【CS231n】Neural Networks Part 3: Learning and Evaluation

機械学習

Stanford大の教材CS231nを使ってNNやCNNを学んでいる．
前回の記事では、層の結合やデータやloss functionなどNNの静的構造について確認した。
本記事では、NNのダイナミクス（パラメータを学習するプロセスやハイパーパラメータの決定方法）について学ぶ。

Gradient checks

  • gradient checkは解析的勾配を数値的勾配を比較すること
    • 実装すると結構複雑で、error-proneである
    • 以下でtipsを述べる

数値的勾配の計算にはcentered formulaを使うこと
  • 数値的勾配を評価するときには通常以下の式を使う {} $$ \frac{d f(x)}{d x} = \frac{f(x + h) - f(x)}{h} $$

  • しかしcentered differenceの式を使った方が良い {} $$ \frac{d f(x)}{d x} = \frac{f(x + h) - f(x - h)}{2h} $$

relative errorを数値的勾配と解析的勾配の比較に使うこと
  • 数値的勾配{f_{n}^{'}}と解析的勾配{f_{a}^{'}}をどう比較するか
    • 勾配のオーダーに基づいて「同じ」かどうか比較するには、{|f_{a}^{'} - f_{n}^{'}|}ではなく相対誤差を使う。
      • 大きさに対する差の比 {} $$ \frac{|f_{a}^{'} - f_{n}^{'}|}{\max(|f_{a}^{'}|, |f_{n}^{'}|)} $$

  • 相対誤差 > 1e-2 のとき、勾配は誤り
  • 1e-2 > 相対誤差 > 1e-4 のときはダメ
  • 1e-4 > 相対誤差 のときkinksがあるときは問題ない。kinksがないとダメ
  • 1e-7 > 相対誤差 のとき問題ない

倍精度表現を使うこと
  • 単精度はダメ
    • 正しい計算処理をしていても、相対誤差が大きくなる

浮動小数点演算の有効な範囲で計算すること

微分不可能な点（kink)に注意
  • kinkは微分不可能な部分のこと
    • ReLUやSVM lossやMaxout neuronなどに存在

  • ReLUの{x = -1e6}での勾配を調べると0のはず
  • しかし数値的勾配は、{f(x+h)}を計算し、kinkを超えるときには、0にならない

少数のdatapointsを使うこと
  • 上記kinksの問題を回避するためには、2,3種の点のみを使うようにすればよい
  • 高速で効率的にgradient checkできる

step size hに注意すること
  • 小さければよいという問題ではない。
    • 小さくしていくと、精度が悪くなる
  • hは1e-4~1e-6の間がよい

gradient check
  • 初期化時は、データが恣意的であるため正しくみえてしまうことがある
  • NNが学習し始めたときなどに行うとよい

regularization(正規化)がデータをoverwhelmしないこと
  • loss fucntionがdata lossとregularization lossの和であるとき、regularizationの影響が強くなることがある
    • loss gradientが正しくなくなる
  • regularizationの項を一旦消して、data lossのみで検証しておくこと

dropout/augmentationsを効果を消しておくこと
  • gradient checkのときには、NNへの効果を極小にすること
    • dropoutやrandom data augmentationsを消しておく

幾つかの次元だけでチェック
  • パラメータの次元は100万を超えることがある.
    そういうときには、幾つかの次元で結果が正しいことを確かめて良い

Sanity checks

  • 高価な最適化に挑む前に次のことをチェックすること
最初のパラメータでlossが正しいか確認すること
  • 正規化の強さを0にして、data lossだけを試すこと
    • もし正しくなければ、初期化が失敗している
  • 正しければ、正規化の強さを上げる
データの一部分に対して学習させる
  • dataset全体に対して学習させる前に、ほんの一部のデータに対して学習させてみる
  • 小さいdatasetで過学習するときには、大きいdatasetでも過学習してしまう

Babysitting the learning process

  • NNの学習時に確認すべき変数がいくつかある
    これをみると学習過程がわかったり、ハイパーパラメータの設定値による違いが見て取れたりする

  • 以下のグラフのx軸はエポック(epoch）を表す
    • 何回一つのデータが学習に使われたかを示す

Loss function

  • lossは使いやすい変数
  • 下図はlossの変遷を示す
    • learning rateの違いも現れている
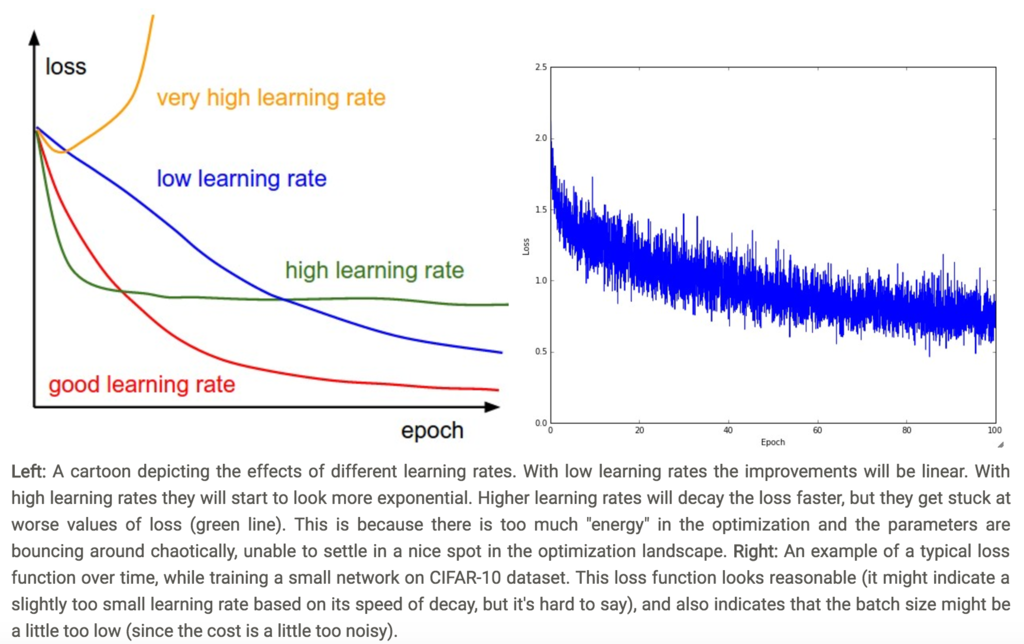f:id:yusuke_ujitoko:20170110214439p:plain (CS231nより引用)

  • lossの振動の量はbatch sizeに関連がある(上図）
    • batch sizeが1のとき振動が激しくなる
    • batch sizeが全データセットのとき、振動は最小になる

Train/Val accuracy

  • 次に重要な変数はvalidationとtrainingのaccuracy
  • これをみると、モデルに過学習しているかがわかる
f:id:yusuke_ujitoko:20170110214947p:plain (CS231nより引用)

Ratio of weights:updates

  • 最後に確認するのは、値の大きさに対する更新の大きさの比
    (生の勾配ではなく、更新であることに注意）

  • ヒューリスティックには、この比は1e-3程度になる
    • これより低いとlearning rateは小さすぎる
    • これより高いとlearning rateが高すぎる

Activation/Gradient distributions per layer

  • 初期化が失敗すると、学習が進まなくなる
  • この症状はactivation/gradient のヒストグラムを描くと発見できる

First-layer Visualizations

  • 画像が対象の場合は、1層目を可視化するとよい
f:id:yusuke_ujitoko:20170110221428p:plain (CS231nより引用)

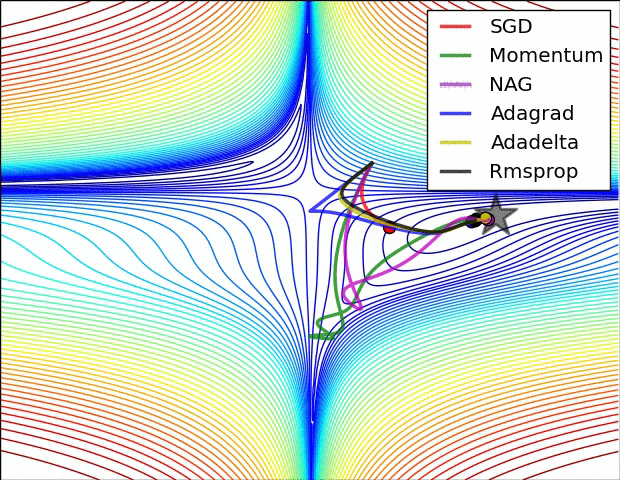
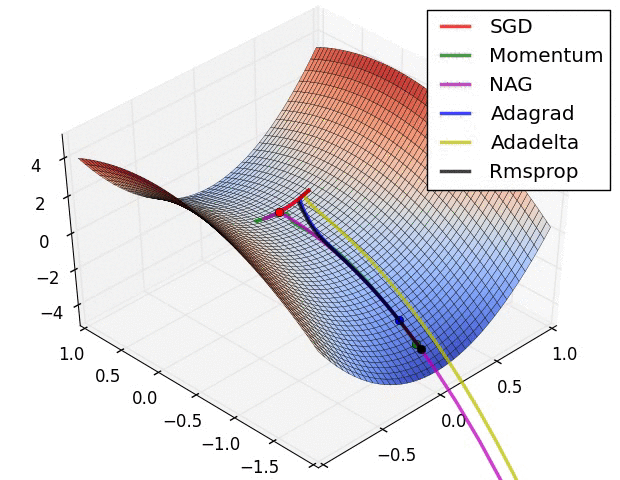
Parameter updates

  • backpropagationで計算した勾配は、パラメータ更新に使われる
  • この節ではパラメータ更新のテクニックについてみていく

SGD and bells and whistles

Vanilla update
  • 更新の一番シンプルな方法は、勾配がマイナスの方向へパラメータを動かすこと
# Vanilla update
x += - learning_rate * dx

Momentum update
  • Momentum updateは物理的なアプローチ。
    • lossを高地とみなして、ボールを地上に転がしていくイメージ

  • 勾配は位置ではなく、速度にのみ影響する
  • 速度が位置へ影響する
# Momentum update
v = mu * v - learning_rate * dx # integrate velocity
x += v # integrate position

Nesterov Momentum
  • Momentum updateの改良版
  • アイデア
    • momentumでは一周期でpython mu * vだけ移動する
    • なので、この移動先での勾配を予め計算し利用する
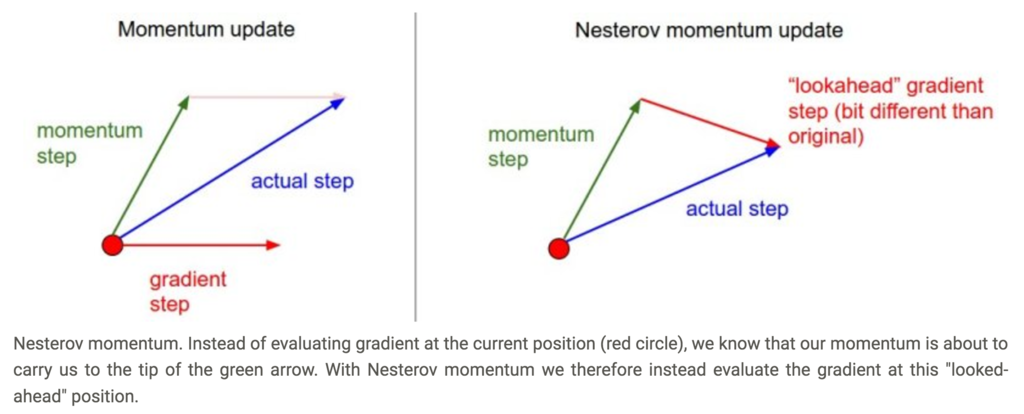f:id:yusuke_ujitoko:20170110223118p:plain (CS231nより引用)

Annealing the learning rate
  • 学習時にlearning rateを操作することは有効
  • 以下の3つのテクニックがある

  • step decay
    • 一定のエポックごとに、learning rateを減少させる
      • 例えば5エポックごとに半減させるなど
    • ハイパーパラメータは問題に依存

  • exponential decay
    • 指数関数的にlearning rateを減少させる
    • {\alpha = \alpha_{0} e^{-kt}}
      • {\alpha_{0}, k}はハイパーパラメータ

  • 1/t decay
    • {\alpha = \alpha_{0}/(1 + kt)}でlearning rateを操作
Second order methods
  • 2番人気の最適化法はNewton法である {} $$ x \ \ \leftarrow \ \ x - [H f(x)]^{-1} \nabla f(x) $$

(省略）

Pre-parameter adaptive learning rate methods
  • これまで見てきた手法では全部のlearning rateに対して等しく操作していた
  • 一方で、適応的にlearning rateをチューニングすることも可能

  • Adagradはadaptive learning rate method
    • 勾配が大きかった重みはlearning rateをより小さくする
# Assume the gradient dx and parameter vector x
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

  • RMSpropはAdagradを改造したもの
cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

  • AdamはRMSPropにmomentumを加えたもの
m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)
f:id:yusuke_ujitoko:20170110232851p:plain:w400 f:id:yusuke_ujitoko:20170110232858p:plain:w400 (CS231nより引用)

Hyperparameter Optimization

  • NNの学習には多くのハイパーパラメータの設定がつきまとう
    • learning rateの初期値
    • learning rateのdecay設定値
    • regularization（正規化）の強さ

  • 巨大NNの学習には膨大な時間がかかる
    • ハイパーパラメータの探索にも…

  • ハイパーパラメータの範囲
    • 指数的に絞るべし

  • random searchの方がgrid searchよりよい

f:id:yusuke_ujitoko:20170110233858p:plain (CS231nより引用)
  • careful with best values on border

  • 粗いところから細かい方へ
  • Bayesian Hyperparameter Optimization

Evaluation

Model Ensembles

  • 独立したモデルをtrainingし、
  • test時にはそれらの予測の平均をとること
  • ensembleするモデルの数が増えるほど、パフォーマンスは単調に良くなる (ただし時間はかかる）

  • モデルを組み合わせる方法は幾つかある
同じモデルを異なる初期値で
  • 最良のハイパーパラメータを探索し、
  • 異なる初期値をもたせて複数のモデルをtrainingする

  • この手法の欠点は、初期値しか変化がないこと
良いモデルを組み合わせる
  • 最良のハイパーパラメータを探索し、
  • 良かった幾つかのモデルを選び、結果を平均化する

  • この手法の欠点は、最適でないモデルも含まれること
1つのモデルを異なるcheckpointで
  • trainingが高価なら、同じモデルの異なる時期をピックアップする
  • 明らかに多様性に欠く。

training時のパラメータの平均をとる
  • モデルのsmoothed version

Summary

NNを学習させるためには、以下が重要

  • gradient checkによりアルゴリズムのミスをチェック
  • sanity checkとして以下を確認
    • 最初のloss
    • 小さいデータセットでtrainingのaccuracyが100%
  • training中に以下を監視しておく
    • loss
    • training/validation accuracy
    • updateの大きさとパラメータの大きさの比
  • 2つのオススメのパラメータ更新法は
    • SGD+Nesterov Momentum
    • Adam
  • learning rateを減少させること
  • ハイパーパラメータをrandom searchで探すこと
    • 最初は粗く、次第に細かくしていく
  • モデルを調和させること

理解できなかった内容

This requires you to evaluate the loss function twice to check every single dimension of the gradient (so it is about 2 times as expensive), but the gradient approximation turns out to be much more precise. To see this, you can use Taylor expansion of f(x+h)f(x+h) and f(x−h)f(x−h) and verify that the first formula has an error on order of O(h)O(h), while the second formula only has error terms on order of O(h2)O(h2) (i.e. it is a second order approximation).

さらに踏み込んだ学習をするには

次の記事

yusuke-ujitoko.hatenablog.com

まとめ

yusuke-ujitoko.hatenablog.com