【CS231n】Putting it together: Minimal Neural Network Case Study

Stanford大の教材CS231nを使ってNNやCNNを学んでいる．
この記事では、toy Neural Networkを実装する。
最初にシンプルなlinear classifierを作り、その次に2層NNへ拡張する

Generating some data

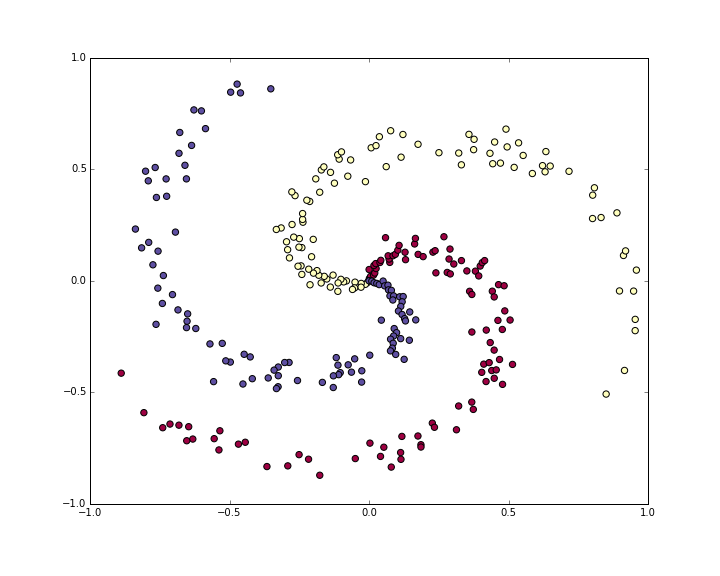
簡単に線形分離できないdatasetを生成する
例として渦状のデータとする
- クラスごとに100点生成

N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels
for j in xrange(K):
  ix = range(N*j,N*(j+1))
  r = np.linspace(0.0,1,N) # radius
  t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
  X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
  y[ix] = j
# lets visualize the data:
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)

f:id:yusuke_ujitoko:20170111195434p:plain:w500

(CS231nより引用)

Training a Softmax Linear Classifier

Initialize the parameters

パラメータ生成と初期化
- python D = 2は次元
- python K = 3は分類クラスの数

# initialize parameters randomly
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))

Compute the class scores

linear classifierを作るので、行列-ベクトル積を計算する

# compute class scores for a linear classifier
scores = np.dot(X, W) + b

2次元の300個の点なので、python scoresは[300 * 3]というサイズ
- 各行はそれぞれのクラスの点を保持（blue, red, yellow)

Compute the loss

loss functionの計算
- クラスごとのscoresがどのくらい満たされてないかを示す
ここではloss functionにsoftmaxのcross-entropy loss(交差エントロピー損失)を使う
- ${f}$ はクラスごとのscore、 ${}$ $$ L_{i} = - \log \frac{e^{f_{y_{i}}}}{\sum_{j} e^{f_{j}}} $$

logの中身は、真のクラスの正規化された確率を示す
- 真のクラスのscoreが小さければ、lossは無限になる
- 逆に大きければ、0に近づく
完全なSoftmax classifier loss は、cross-entropy lossの平均と、正規化項の和になる ${}$ $$ L = \frac{1}{N} \sum_{i} L_{i} + \frac{1}{2} \sum_{k} \sum_{l} W_{k,l}^{2} $$

scoreをもとにlossを計算する

# get unnormalized probabilities
exp_scores = np.exp(scores)
# normalize them for each example
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)

クラス分類ごとに正規化する

corect_logprobs = -np.log(probs[range(num_examples),y])

完全なlossは上記のlogをとって平均化したものに、正規化 lossを足したもの

# compute the loss: average cross-entropy loss and regularization
data_loss = np.sum(corect_logprobs)/num_examples
reg_loss = 0.5*reg*np.sum(W*W)
loss = data_loss + reg_loss

Computing the Analytic Gradient with Backpropagation

lossを最小化したい。そのためにgradient descentする
- ランダムなパラメータから始め、
- loss functionの勾配を評価し、
- どうパラメータを移動すればよいか判断する

中間変数[tex:{p}}を導入する
- 確率を表現 ${}$ $$ p_{k} = \frac{e^{f_{y_{i}}}}{\sum_{j} e^{f_{j}}} \ \ \ \ \ \ \ \ \ L_{i} = - \log (p_{y_{i}}) $$

を求めたい
- ${L}$ は ${p}$ に依存しており、 ${p}$ は ${f}$ に依存している
- 連鎖律を使って求めていく ${}$ $$ \frac{\partial L_{i}}{\partial f_{k}} = p_{k} - 1(y_{i} = k) $$

スコアの勾配python dscoresを得る

dscores = probs
dscores[range(num_examples),y] -= 1
dscores /= num_examples

スコアの勾配から重み ${W}$ と ${b}$ の勾配を算出していく

dW = np.dot(X.T, dscores)
db = np.sum(dscores, axis=0, keepdims=True)
dW += reg*W # don't forget the regularization gradient

Performing a parameter update

勾配が減る方向に動かす

# perform a parameter update
W += -step_size * dW
b += -step_size * db

Putting it all together: Training a Softmax Classifier

全てを一つにまとめる。
これがsoftmax classifierの全体

#Train a Linear Classifier
# initialize parameters randomly
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))

# some hyperparameters
step_size = 1e-0
reg = 1e-3 # regularization strength

# gradient descent loop
num_examples = X.shape[0]
for i in xrange(200):
  
  # evaluate class scores, [N x K]
  scores = np.dot(X, W) + b 
  
  # compute the class probabilities
  exp_scores = np.exp(scores)
  probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]
  
  # compute the loss: average cross-entropy loss and regularization
  corect_logprobs = -np.log(probs[range(num_examples),y])
  data_loss = np.sum(corect_logprobs)/num_examples
  reg_loss = 0.5*reg*np.sum(W*W)
  loss = data_loss + reg_loss
  if i % 10 == 0:
    print "iteration %d: loss %f" % (i, loss)
  
  # compute the gradient on scores
  dscores = probs
  dscores[range(num_examples),y] -= 1
  dscores /= num_examples
  
  # backpropate the gradient to the parameters (W,b)
  dW = np.dot(X.T, dscores)
  db = np.sum(dscores, axis=0, keepdims=True)
  
  dW += reg*W # regularization gradient
  
  # perform a parameter update
  W += -step_size * dW
  b += -step_size * db

これを実行すると以下の出力を得る

iteration 0: loss 1.096956
iteration 10: loss 0.917265
iteration 20: loss 0.851503
iteration 30: loss 0.822336
iteration 40: loss 0.807586
iteration 50: loss 0.799448
iteration 60: loss 0.794681
iteration 70: loss 0.791764
iteration 80: loss 0.789920
iteration 90: loss 0.788726
iteration 100: loss 0.787938
iteration 110: loss 0.787409
iteration 120: loss 0.787049
iteration 130: loss 0.786803
iteration 140: loss 0.786633
iteration 150: loss 0.786514
iteration 160: loss 0.786431
iteration 170: loss 0.786373
iteration 180: loss 0.786331
iteration 190: loss 0.786302

190回の反復で収束する
このtraining setを評価する

# evaluate training set accuracy
scores = np.dot(X, W) + b
predicted_class = np.argmax(scores, axis=1)
print 'training accuracy: %.2f' % (np.mean(predicted_class == y))

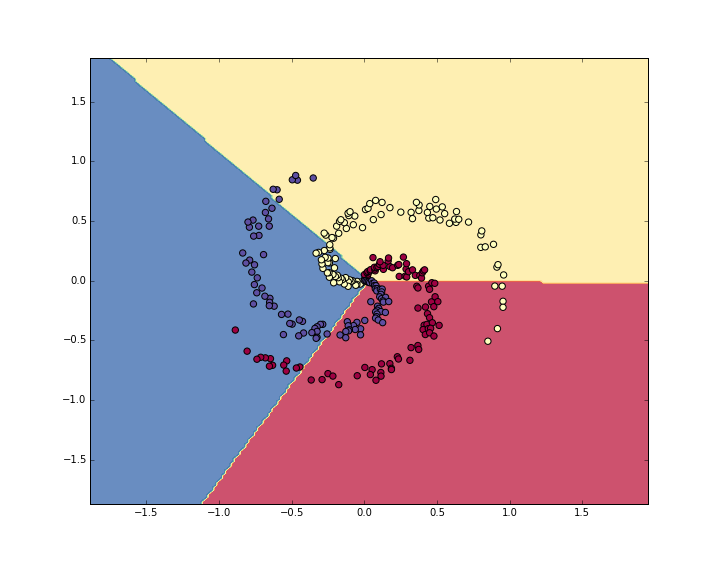
49%を得る。そこまで良くはない。

f:id:yusuke_ujitoko:20170111211313p:plain

(CS231nより引用)

無理やり線形分離している…

Training a Neural Network

NNで同じ課題に取り組んでみる

隠れ層が必要なので、その分重みとバイアスを用意

# initialize parameters randomly
h = 100 # size of hidden layer
W = 0.01 * np.random.randn(D,h)
b = np.zeros((1,h))
W2 = 0.01 * np.random.randn(h,K)
b2 = np.zeros((1,K))

scoreを計算するforward passも2層分

# evaluate class scores with a 2-layer Neural Network
hidden_layer = np.maximum(0, np.dot(X, W) + b) # note, ReLU activation
scores = np.dot(hidden_layer, W2) + b2

2層目のパラメータの勾配を計算

# backpropate the gradient to the parameters
# first backprop into parameters W2 and b2
dW2 = np.dot(hidden_layer.T, dscores)
db2 = np.sum(dscores, axis=0, keepdims=True)

1層目のパラメータの勾配を計算するために、逆伝播していく

dhidden = np.dot(dscores, W2.T)

ReLU関数をbackprop

# backprop the ReLU non-linearity
dhidden[hidden_layer <= 0] = 0

1層目のパラメータの勾配を計算

# finally into W,b
dW = np.dot(X.T, dhidden)
db = np.sum(dhidden, axis=0, keepdims=True)

パラメータの更新は変更なし
以下が完全なコード

# initialize parameters randomly
h = 100 # size of hidden layer
W = 0.01 * np.random.randn(D,h)
b = np.zeros((1,h))
W2 = 0.01 * np.random.randn(h,K)
b2 = np.zeros((1,K))

# some hyperparameters
step_size = 1e-0
reg = 1e-3 # regularization strength

# gradient descent loop
num_examples = X.shape[0]
for i in xrange(10000):
  
  # evaluate class scores, [N x K]
  hidden_layer = np.maximum(0, np.dot(X, W) + b) # note, ReLU activation
  scores = np.dot(hidden_layer, W2) + b2
  
  # compute the class probabilities
  exp_scores = np.exp(scores)
  probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]
  
  # compute the loss: average cross-entropy loss and regularization
  corect_logprobs = -np.log(probs[range(num_examples),y])
  data_loss = np.sum(corect_logprobs)/num_examples
  reg_loss = 0.5*reg*np.sum(W*W) + 0.5*reg*np.sum(W2*W2)
  loss = data_loss + reg_loss
  if i % 1000 == 0:
    print "iteration %d: loss %f" % (i, loss)
  
  # compute the gradient on scores
  dscores = probs
  dscores[range(num_examples),y] -= 1
  dscores /= num_examples
  
  # backpropate the gradient to the parameters
  # first backprop into parameters W2 and b2
  dW2 = np.dot(hidden_layer.T, dscores)
  db2 = np.sum(dscores, axis=0, keepdims=True)
  # next backprop into hidden layer
  dhidden = np.dot(dscores, W2.T)
  # backprop the ReLU non-linearity
  dhidden[hidden_layer <= 0] = 0
  # finally into W,b
  dW = np.dot(X.T, dhidden)
  db = np.sum(dhidden, axis=0, keepdims=True)
  
  # add regularization gradient contribution
  dW2 += reg * W2
  dW += reg * W
  
  # perform a parameter update
  W += -step_size * dW
  b += -step_size * db
  W2 += -step_size * dW2
  b2 += -step_size * db2

これを実行すると以下の出力を得る

iteration 0: loss 1.098744
iteration 1000: loss 0.294946
iteration 2000: loss 0.259301
iteration 3000: loss 0.248310
iteration 4000: loss 0.246170
iteration 5000: loss 0.245649
iteration 6000: loss 0.245491
iteration 7000: loss 0.245400
iteration 8000: loss 0.245335
iteration 9000: loss 0.245292

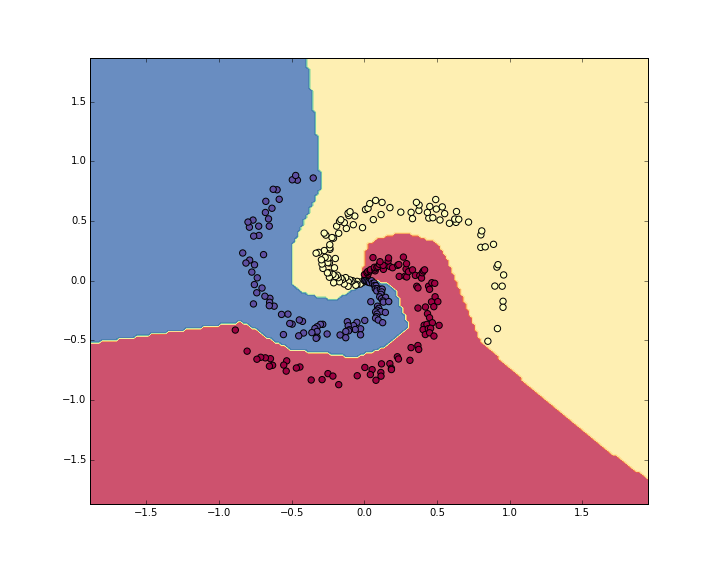
training accuercyは98%

# evaluate training set accuracy
hidden_layer = np.maximum(0, np.dot(X, W) + b)
scores = np.dot(hidden_layer, W2) + b2
predicted_class = np.argmax(scores, axis=1)
print 'training accuracy: %.2f' % (np.mean(predicted_class == y))