Stanford大の教材CS231nを使ってNNやCNNを学んでいる.
本記事では,Backpropagation(誤差逆伝播法)を中心に扱う.
Introduction
- 本セクションでは勾配とbackpropagationを直観的に理解してみる
- backpropagationとは、chain rule(連鎖律)を反復的に利用して勾配を計算する方法のこと
- backpropagationはNeural Networksの典型的なケースに適用できる
シンプルな例で勾配を解釈してみる
乗算
という関数の微分を考える
$$ f(x,y) = xy \ \ \rightarrow \ \ \frac{\partial f}{\partial x} = y, \ \ \ \
\frac{\partial f}{\partial y} = x $$
- 解釈
- 微分は「着目する変数に対して、ある地点での関数の変化率」を示す
$$ \frac{d f(x)}{d x} = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} $$
- 微分は「着目する変数に対して、ある地点での関数の変化率」を示す
- 微分と偏微分は異なることに注意
- 勾配
は偏微分のベクトルとなる
$$ {\nabla f = [\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}] = [y, x]} $$
加算
- 加算に対しても微分を考えてみる
$$ f(x,y) = x + y \ \ \rightarrow \ \ \frac{\partial f}{\partial x} = 1 , \ \ \ \
\frac{\partial f}{\partial y} = 1 $$
= y), \ \ \ \ \frac{\partial f}{\partial y} = 1 \ \ (y >= x) $$
- 例えばxがで,yが2であるとき,
- maxは4
- yの値に無関係
Compound expressions, chain rules, backpropagation
- もう少し複雑な式を考えてみる
- たとえば,
- 解析的に微分するのは簡単
- でもbackpropagationの本質を理解するために,別のアプローチをとってみる
- 細かく刻んでいく
と
に分解する
は
と
の積なので,
,
となる.
は
と
の和なので,
,
となる.
- code例
# set some inputs x = -2; y = 5; z = -4 # perform the forward pass q = x + y # q becomes 3 f = q * z # f becomes -12 # perform the backward pass (backpropagation) in reverse order: # first backprop through f = q * z dfdz = q # df/dz = q, so gradient on z becomes 3 dfdq = z # df/dq = z, so gradient on q becomes -4 # now backprop through q = x + y dfdx = 1.0 * dfdq # dq/dx = 1. And the multiplication here is the chain rule! dfdy = 1.0 * dfdq # dq/dy = 1
- 計算グラフに視覚化すると下記のようになる
- 入力から出力(左から右)をforward passという
- 出力から入力(右から左)をbackward passという
- backward passはbackpropagationを示しており,再帰的に出力から入力へchain ruleを適用していく
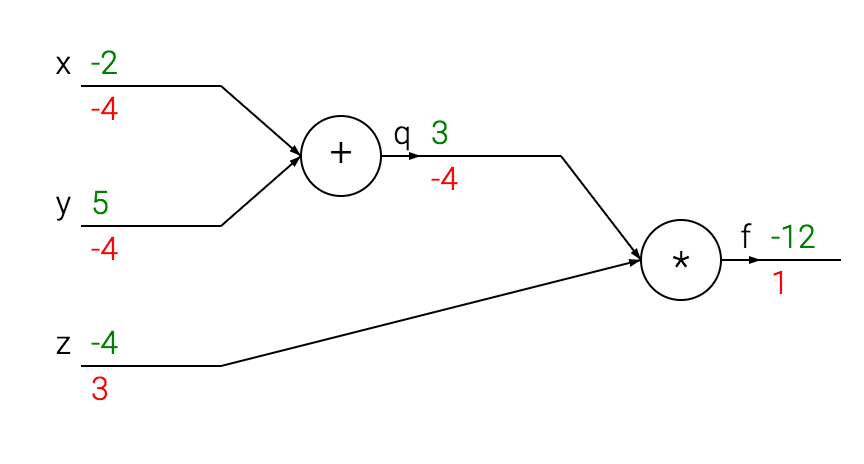 (CS231nより引用)
(CS231nより引用)
Intuitive understanding of backpropagation
- backpropagationは局所的な処理のかたまり
- 計算グラフの1つのノードを見ると,入力をもとに以下の2つを計算することができる
- 出力値
- 入力の出力に対する勾配
- 計算グラフ全体に無関係に1ノードでの局所的な計算は可能
- 計算グラフの1つのノードを見ると,入力をもとに以下の2つを計算することができる
- foward passの後,backpropagation
- 各ノードの勾配を結合していくと計算グラフ全体の勾配がわかる
- chain rule(連鎖律)の原理
Modularity: Sigmoid example
- どんな微分関数もノードとしてはたらく.
- 複数のノードをまとめて1つのノードとしてみなすことができる
例としてこの関数を見ていく
の内積をsigmoid functionで処理する関数
$$ f(w, x) = \frac{1}{1 + \exp(-(w_{0} x_{0} + w_{1} x_{1} + w2))} $$
(その前に,必要な知識を補充)
$$ \begin{align} f(x) = \frac{1}{x} \rightarrow \frac{d f}{d x} = - \frac{1}{x^{2}} \\ f_{c}(x) =c + x \rightarrow \frac{d f}{d x} = 1 \\ f(x) = \exp(x) \rightarrow \frac{d f}{d x} = \exp(x) \\ f_{a}(x) =a x \rightarrow \frac{d f}{d x} = a \\ \end{align} $$
関数全体を計算グラフにすると下図のようになる.
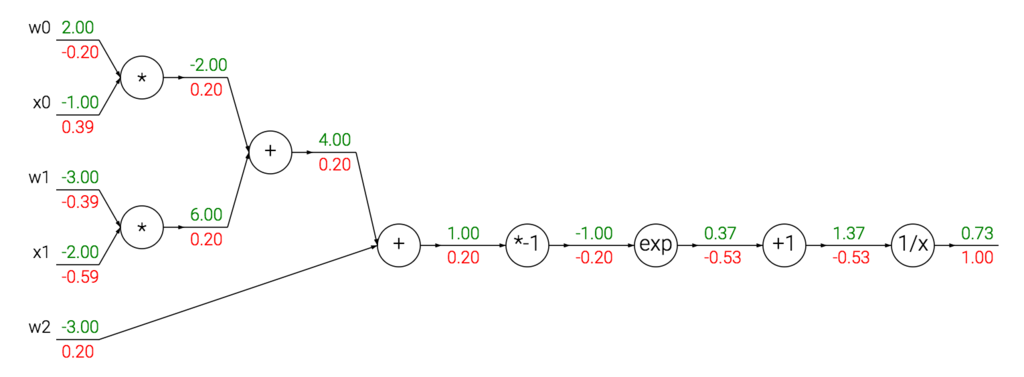 (CS231nより引用)
(CS231nより引用)
- たとえば
を入力したときには,勾配は(1 - 0.73) * 0.73 ~~ 0.2となる
- 複数のノードからなるものでも,入力と出力の勾配を見るときには,全体を1つのノードとして見たほうが楽
- backpropagationを計算して,
や
を計算するコード
w = [2,-3,-3] # assume some random weights and data x = [-1, -2] # forward pass dot = w[0]*x[0] + w[1]*x[1] + w[2] f = 1.0 / (1 + math.exp(-dot)) # sigmoid function # backward pass through the neuron (backpropagation) ddot = (1 - f) * f # gradient on dot variable, using the sigmoid gradient derivation dx = [w[0] * ddot, w[1] * ddot] # backprop into x dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot] # backprop into w # we're done! we have the gradients on the inputs to the circuit
- forward passを細かくしておくと,backpropが容易に行える
Backprop in practice: Staged computation
- 以下の関数を例として考える
- まず中間生成物を経由しながらforward passを書き下す
x = 3 # example values y = -4 # forward pass sigy = 1.0 / (1 + math.exp(-y)) # sigmoid in numerator #(1) num = x + sigy # numerator #(2) sigx = 1.0 / (1 + math.exp(-x)) # sigmoid in denominator #(3) xpy = x + y #(4) xpysqr = xpy**2 #(5) den = sigx + xpysqr # denominator #(6) invden = 1.0 / den #(7) f = num * invden # done! #(8)
- それぞれの中間生成物に対する出力の微分を順に計算していく.
# backprop f = num * invden dnum = invden # gradient on numerator #(8) dinvden = num #(8) # backprop invden = 1.0 / den dden = (-1.0 / (den**2)) * dinvden #(7) # backprop den = sigx + xpysqr dsigx = (1) * dden #(6) dxpysqr = (1) * dden #(6) # backprop xpysqr = xpy**2 dxpy = (2 * xpy) * dxpysqr #(5) # backprop xpy = x + y dx = (1) * dxpy #(4) dy = (1) * dxpy #(4) # backprop sigx = 1.0 / (1 + math.exp(-x)) dx += ((1 - sigx) * sigx) * dsigx # Notice += !! See notes below #(3) # backprop num = x + sigy dx += (1) * dnum #(2) dsigy = (1) * dnum #(2) # backprop sigy = 1.0 / (1 + math.exp(-y)) dy += ((1 - sigy) * sigy) * dsigy #(1) # done! phew
- 注意点
- foward passにおける中間生成物の値をキャッシュしておく
- Gradients add up at forks
Patterns in backward flow
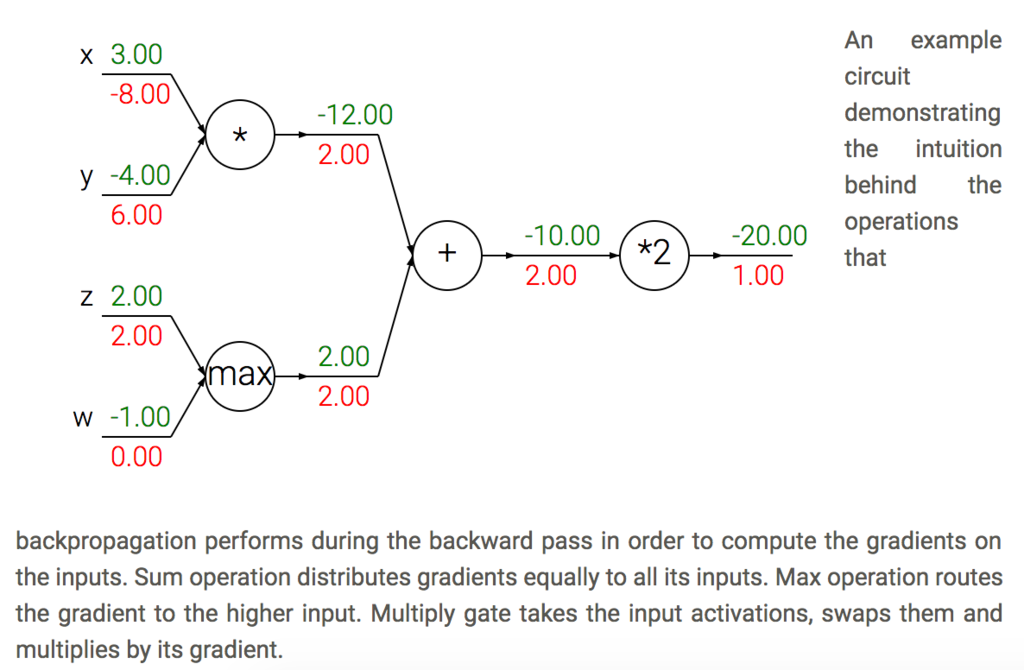 (CS231nより引用)
(CS231nより引用)
- 逆伝播(backward-flowing)は直観的に理解できる
- NN(ニューラルネットワーク)でよく使われる3つの操作について見ていく
- 加算
- 乗算
- max
- NN(ニューラルネットワーク)でよく使われる3つの操作について見ていく
- 加算ノード
- 出力に関する勾配を受取り,入力元にそのまま流していく
- foward passでの値に無関係
- (加算における局所的な勾配は1である)
- 上図を見ると,2の勾配を受け取ると,そのまま入力に流している
- 出力に関する勾配を受取り,入力元にそのまま流していく
- maxノード
- 加算ノードと違い,forward passで最大値であった入力元にのみ,勾配をそのまま渡す
- なぜかというと,局所的な勾配は最大値に対してのみ1で,それ以外は0となる
- 上図の例で確認すると,maxノードはzには2を渡し,wは0を渡している
- 乗算ノード(少し直観的でない)
- 局所的な勾配は互いの入力値になる
- 連鎖律により,出力に対する流れてきた勾配に,局所的な勾配を掛けることとなる
- 上図の例を見ると,xに関する出力の勾配は-8(-4 * 2)
- 直観的でない効果と結果
Gradients for vectorized operation
- これまでの例はスカラ値だったが,同じ方法は行列やベクトル操作にも適用できる
- ただし次元と転置には注意すること
行列積の勾配
- 一番トリッキーなのは行列積
- 次元分析(dimension analysis)すること!
- 下記の
や
の公式を覚える必要はない
- 下記の
# forward pass W = np.random.randn(5, 10) X = np.random.randn(10, 3) D = W.dot(X) # now suppose we had the gradient on D from above in the circuit dD = np.random.randn(*D.shape) # same shape as D dW = dD.dot(X.T) #.T gives the transpose of the matrix dX = W.T.dot(dD)
- たとえば
を知りたいとき
と
は同じ次元である,ことを利用すれば,
の内積から導かれることがわかる
- 行列,ベクトルの微分に関してErik Learned-Millerが関連記事を書いているので参考にすべし
Summary
- 以下の概念を直観的にとらえた
- 勾配が何を意味するのか
- 計算グラフの中で逆伝播をどう行うのか
- 計算グラフのどのノードが値を増やしたり,減らしたりするか
- backpropagationの実装ためのstaged computation(段階的な計算処理)の重要性を確認した
- 関数をモジュールに分割して,局所的な勾配を計算し,chain ruleで結合する
理解できなかった内容
Gradients add up at forks. The forward expression involves the variables x,y multiple times, so when we perform backpropagation we must be careful to use += instead of = to accumulate the gradient on these variables (otherwise we would overwrite it). This follows the multivariable chain rule in Calculus, which states that if a variable branches out to different parts of the circuit, then the gradients that flow back to it will add.
さらに踏み込んだ学習をするには
Automatic differentiation in machine learning: a survey