【CS231n】Neural Networks Part 2: Setting up the Data and the Loss

Stanford大の教材CS231nを使ってNNやCNNを学んでいる．
本記事では，Neural Network(NN)を中心に扱う．

Setting up the data and the model

Linear Classification用からNN用へscore functionの拡張
- linear mappingを繰り返しの中にnon-linearityを織り交ぜる

Data Preprocessing

入力データ ${X}$ に対して3つの代表的な前処理がある

Mean subtraction
- 個々の特徴から平均値を引く処理
- 幾何的に解釈すると、データの集まりの中心を原点に持ってくる処理でもある

Nomalization
- 次元を正規化すること
- 2つの代表的な方法がある
  - 標準偏差で入力データを割る方法
  - 最小値と最大値を-1～1にする方法

f:id:yusuke_ujitoko:20170109190357p:plain

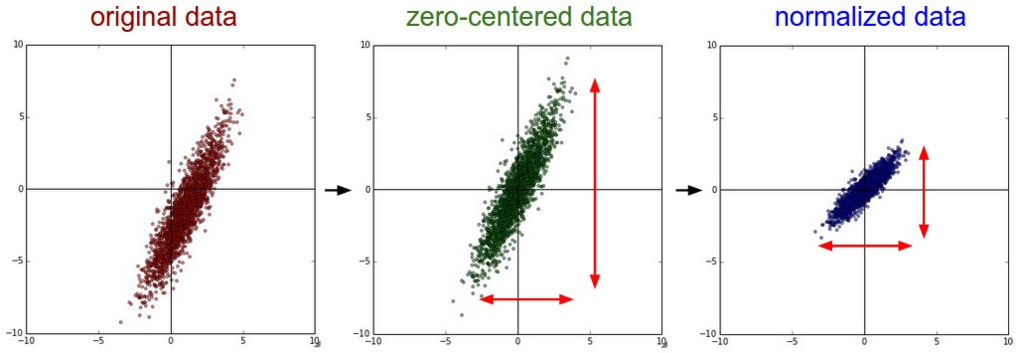(CS231nより引用)

PCAとWhitening
- (前提としてmean subtractionされている状態とする）
- 共分散行列を計算する

# Assume input data matrix X of size [N x D]
X -= np.mean(X, axis = 0) # zero-center the data (important)
cov = np.dot(X.T, X) / X.shape[0] # get the data covariance matrix

PCAとWhitening（続き）
- 共分散行列
  - (i,j)要素はi行目とj列目のデータの共分散を保持
- 求めた共分散行列から特異値分解する

U,S,V = np.linalg.svd(cov)

PCAとWhitening（続き）
- 入力データをdecorrelateする

Xrot = np.dot(X, U) # decorrelate the data

PCAとWhitening（続き）
- 次元を削減するために上位の固有ベクトルのみ使う
- Principal Component Analysis(PCA)次元削減とよばれる
- これによりもともとのデータセット[N * D]から[N * 100]へ削減できる
  この100個は重要な分散を保持している

Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced becomes [N x 100]

whitening
- 全次元に対して固有値で割ってスケールを正規化すること
- もともとmultivariable gaussianだったデータの広がりを、0平均、identitity covariance matrixをもつgaussianとする操作でもある

# whiten the data:
# divide by the eigenvalues (which are square roots of the singular values)
Xwhite = Xrot / np.sqrt(S + 1e-5)

f:id:yusuke_ujitoko:20170109192819p:plain

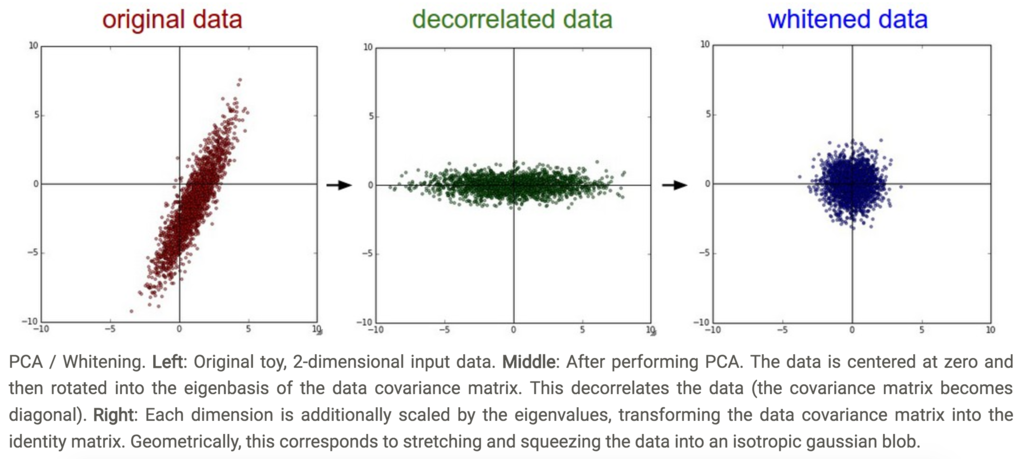(CS231nより引用)

この正規化処理によるデータの変化をCIFAR-10で検証したのが下図

f:id:yusuke_ujitoko:20170109193203p:plain

(CS231nより引用)

落とし穴
- 前処理の統計処理はtraining dataのみで計算して、その後でvalidation dataやtest dataに適用すること
- 全体に対して計算処理して、あとからtraining/validaiton/testと分割してはいけない

Weight Initialization

重みを0で初期化してはいけない
- 全neuronが同じ出力をしてしまい、同じ勾配を逆伝播時に算出し、同じようにパラメータを更新してしまう

小さい値で初期化する
- なぜ??

分散を1/sqrt(n)により補正する
- neuronの出力の分散を1にするため、重みに1/sqrt(n)掛ける

sparse initialization

initializing the biases
- バイアスは0に初期化してよい
  asymmetry breakingは重みの方で行えばよい

実用上の方策としては、ReLUユニットを使い、pythonw = np.random.randn(n) * sqrt(2.0/n)（He et al.）とすればよい

Batch Normalization
- 全結合層の後にBatchNorm層を置く
- 初期化に失敗したNNでも、いい結果を残せるかもしれない

Regularization

NNの過学習を防ぐ方法は幾つかある
- L2 regularization
- L1 regularization
- max norm constraints
- dropout

L2 regularization（L2正規化）
- NNの各重み ${w}$ に ${\frac{1}{2} \lambda w^{2}}$ を掛ける
- ${\lambda}$ は正規化の強さ

L1 regularization（L1正規化）
- 各重み ${w}$ に ${\lambda |w|}$ を足す

L1とL2を組み合わせることも可能(Elastic net regularization)
- ${\lambda |w| + \frac{1}{2} \lambda w^{2}}$
- L1はzeroに向かわせるはたらきをする
- L2はノイズを混ぜるはたらきをする

max norm constraints
- 重みの最大値を制限してしまう方法
- 各ニューロンの重みベクトル ${\overrightarrow{w}}$ に対して、 ${|| \overrightarrow{w} ||^{2} \leq c}$ を満たすようにする

dropout
- neuronの中の一部を選択的にdeactivateする(下図参照）

f:id:yusuke_ujitoko:20170109210323p:plain

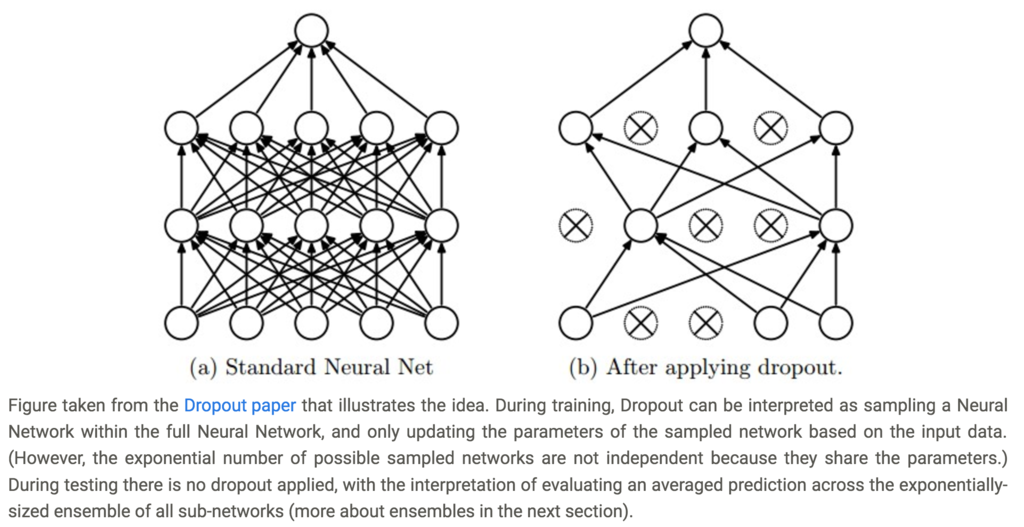(CS231nより引用)

dropoutのコード例

""" Vanilla Dropout: Not recommended implementation (see notes below) """

p = 0.5 # probability of keeping a unit active. higher = less dropout

def train_step(X):
  """ X contains the data """
  
  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = np.random.rand(*H1.shape) < p # first dropout mask
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = np.random.rand(*H2.shape) < p # second dropout mask
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3
  
  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)
  
def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) * p # NOTE: scale the activations
  H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # NOTE: scale the activations
  out = np.dot(W3, H2) + b3

inverted dropoutを使ったほうがコードがシンプルになる
- training時にのみdropoutし、test時のforward passはdropoutしない

""" 
Inverted Dropout: Recommended implementation example.
We drop and scale at train time and don't do anything at test time.
"""

p = 0.5 # probability of keeping a unit active. higher = less dropout

def train_step(X):
  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = (np.random.rand(*H1.shape) < p) / p # first dropout mask. Notice /p!
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = (np.random.rand(*H2.shape) < p) / p # second dropout mask. Notice /p!
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3
  
  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)
  
def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) # no scaling necessary
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  out = np.dot(W3, H2) + b3

biasの正規化は一般的でない

実用上は、L2正規化とdropoutをともに利用するのが一般的

Loss functions

問題が色々ある
分類クラスが多すぎる問題
- 英単語やImageNetの場合などはラベルが多い
- Hierachical Softmaxを使うべき
  - ラベルを木構造化

これまでは一つの答えを選ぶ問題のみ扱ってきた。でもbinary vectorを算出する問題だったら？

Summary

オススメの前処理
- データを中央に寄せ、その平均を0にする
- 特徴に沿って、データを[-1, 1]の範囲に正規化

重みを、標準偏差をとるgaussian distributionとなるよう初期化
- numpyではpython w = np.random.randn(n) * sqrt(2.0/n)

L2正規化とdropoutを使う

batch normalizationを使う

理解できなかった内容

Sparse initialization. Another way to address the uncalibrated variances problem is to set all weight matrices to zero, but to break symmetry every neuron is randomly connected (with weights sampled from a small gaussian as above) to a fixed number of neurons below it. A typical number of neurons to connect to may be as small as 10.

yusuke-ujitoko.hatenablog.com