Boundary Equilibrium GAN（BEGAN）でいらすとや画像を生成してみる

機械学習

このBEGANを使って以下のようないらすとや画像を生成するというのが本記事の主旨。

f:id:yusuke_ujitoko:20170530010053p:plain

完全にmode collapseしてしまった。
結構いろいろ試しているものの、パラメータ調整に今のところ失敗。
悲しい。しくしく。

本論文のcontribution(とIntroに書いてある）

この論文では以下を提案している。

  • 以下の特徴を持つGANの一種(“BEGAN"としている)
    • シンプルかつロバストな構造
    • 高速に収束する
  • DiscriminatorとGeneratorの学習速度のつりあいの制御方法
  • 画像の多様性と質のトレードオフの制御方法
  • 収束の様子を評価する方法

提案手法

BEGANの概要は以下の通り

  • EBGANと同じようにauto-encoderをDiscriminatorとして使う
  • 通常GANのGeneratorは、訓練データと生成データの分布を直接一致させようとするのに対し、 BEGANのGeneratorは、訓練データと生成データ間でauto-encoderの再構成誤差の分布を一致させるように学習させる
    • 再構成誤差の訓練データと生成データ間のWasserstein距離を目的関数として学習させる

auto-encoder用のWasserstein distance

BEGANではauto-encoderの再構成誤差分布を一致させることを目的としている。
この目的に向けて、まずパラメータを定義する。

{\mathcal{L}: \mathbb{R}^{N_{x}} \mapsto \mathbb{R}^{+} }　をauto-encoderの{N_{x}}次元のデータの再構成誤差関数(出力はスカラー）とする。
{\mathcal{D}: \mathbb{R}^{N_{x}} \mapsto \mathbb{R}^{N_{x}} } をauto-encoderそのものの処理(encode、decodeの)関数とする。

これらに基づく、auto-encoderの誤差は {\mathcal{L}(v) = | v - \mathcal{D}(v) |^{\eta} } と表せる。
なおBEGANでは {\eta = 1}を使っている。
十分大きな画像の場合、この再構成誤差はi.i.dとみなせることと中心極限定理から、
画像ごとの再構成誤差は正規分布で近似できることが知られている。
（実際著者らがデータセットで再構成誤差を調べたところ正規分布になったらしい）

さて、再構成誤差が正規分布であると仮定できると、
再構成誤差のWasserstein距離が解析的に計算できる。
訓練データと生成データを、平均 {m_{1,2} \in \mathbb{R}^{p} }・共分散 {C_{1,2} \in \mathbb{R}^{p \times p}}のガウス分布の変量をとすると、
{\mu_{1} = \mathcal{N}(m_{1}, C_{1}) }
{\mu_{2} = \mathcal{N}(m_{2}, C_{2}) }
と表せる。このとき、Wasserstein distanceの二乗は次のように定義できる。 {} $$ W (\mu_{1}, \mu_{2} )^{2} = \mid\mid m_{1} - m_{2} \mid\mid^{2} + tr(C_{1} + C_{2} - 2(C_{2}^{½} C_{1} C_{2}^{½} )^{½} ) $$ さらに次元が1の場合には、 {} $$ W (\mu_{1}, \mu_{2}) = \mid\mid m_{1} - m_{2} \mid\mid_{2}^{2} + (C_{1} + C_{2} - 2 \sqrt{C_{1} C_{2}}) $$ となる。
ここでもうひとつ仮定を入れる。それは、 {\frac{c_{1} + c_{2} - 2 \sqrt{c_{1} c_{2}}}{\mid\mid m_{1} - m_{2} \mid\mid_{2}^{2}}} が定数になるという仮定。 この仮定のもとでは、 {} $$ W (\mu_{1}, \mu_{2}) \propto \mid\mid m_{1} - m_{2} \mid\mid_{2}^{2} \tag{1} $$ とみなせて問題を単純化できる。 （異常に単純化されたが大丈夫か？と思った）

GANの目的関数

Discriminatorがauto-encoderの誤差の距離(1)を最大化するように学習させたい。

  • {\mu_{1}}を訓練データ{x}の誤差{\mathcal{L}(x)}の変量とし、
  • {\mu_{2}}をGeneratorの関数{G}、{N_{x}}次元の一様分布変量{z}における誤差{\mathcal{L}(G(z))}の変量とすると、

誤差の距離(1)を最大化するには以下のいずれかの状況となっている必要がある。 {} $$ \begin{align} (a) \begin{cases} W(\mu_1,\mu_2) \propto m_1 - m_2 \\ m_1 \to \infty \\ m_2 \to 0 \\ \end{cases} (b) \begin{cases} W(\mu_1,\mu_2) \propto m_2 - m_1 \\ m_1 \to 0 \\ m_2 \to \infty \\ \end{cases} \end{align}\ $$ 訓練データの誤差{\mathcal{L}(x)}は0になって欲しいので、(b)を選択する。
（{m_{1}}と{m_{2}}はそれぞれ{\mathcal{L(x)}}と{\mathcal{L}(G(z))}の平均)

さて、DiscriminatorとGeneratorの目的関数を定義しよう。
{\theta_{D}}はDiscriminatorのパラメータ、
{\theta_{G}}はGeneratorのパラメータ、
{z_{D}}と{z_{G}}は{N_{z}}次元のノイズベクトルとすると、
DiscriminatorとGeneratorの目的関数は {} $$ \begin{align} {\mathcal{L}}_{D} &= {\mathcal{L}}(x;\theta_{D}) - {\mathcal{L}}(G(z_{D};\theta_{G});\theta_{D})\\ {\mathcal{L}}_{G} &= {\mathcal{L}}(G(z_{G};\theta_{G});\theta_{D}) \end{align}\ %]]> $$ と定義できる。 この目的関数では、

  • Discriminatorは、訓練データの再構成誤差が小さくなり、一方で生成データの再構成誤差が大きくなることを目指す
  • Generatorは、生成データの再構成誤差が小さくなることを目指している。

この目的関数はWGANのものと似ているが、大きく以下の点で異なっている。

  • 正規分布の誤差の分布を扱っていること
  • Wasserstein distanceの計算を単純化していること。WGANではK-リプシッツ性を必要としていたのに対して提案手法では気にしていない

Equilibrium(平衡）

上記の目的関数をうまく機能させるには、 GとDの学習速度をバランスさせる必要がある。

Generatorによる生成データを訓練データと見分けられないような「釣り合い」の状態は、 誤差分布の期待値は等しくなるはずである。 {} $$ \begin{align} {\mathbb{E}}[{\mathcal{L}}(x)] = {\mathbb{E}}[{\mathcal{L}}(G(z))] \end{align}\ $$ 通常GANでは、この状態を目指すように学習させるのだが、 今回は、{\frac{c_{1} + c_{2} - 2 \sqrt{c_{1} c_{2}}}{\mid\mid m_{1} - m_{2} \mid\mid_{2}^{2}}} が定数になるという仮定を置いたのを思い出してほしい。 この釣り合いの状態では{m_{1} - m_{2} \rightarrow 0}となり仮定が成り立たなくなる。

この問題を解決するために、 釣り合いの状態を目指さず、 {} $$ \begin{align} \gamma = \frac{{\mathbb{E}}[{\mathcal{L}}(G(z))]}{{\mathbb{E}}[{\mathcal{L}}(x)]} \tag{2} \end{align}\ $$ の状態を満たすように、ハイパーパラメータ{\gamma \in (0,1)}を導入し、学習をコントロールする。

BEGAN

以上を踏まえてBEGANの目的関数を、 {} $$ \begin{align} {\mathcal{L}}_{D} &= {\mathcal{L}}(x) - k_{t} \cdot {\mathcal{L}}(G(z_{D})) \tag{3} \\ {\mathcal{L}}_{G} &= {\mathcal{L}}(G(z_{G})) \tag{4} \\ k_{t+1} &= k_{t} + \lambda_{k}(\gamma {\mathcal{L}}(x) - {\mathcal{L}}(G(z_{D})) \tag{5} \end{align}\ $$ としている。
著者らはPropotional Control Theoryという枠組みとして提案しており、 {\gamma{\mathbb{E}} \left[{\mathcal{L}}(x) \right] = {\mathbb{E}} \left[{\mathcal{L}}(G(z))\right] }の釣り合いを保つことを目的としている。

はじめは{k_{0} = 0}と初期化する。 {\lambda_{k}}は{k}のpropotional gainで、0.001を用いている。

この目的関数は、式(2)を保つフィードバック系となっている。
例えば学習初期には、

  • Gは簡単にautoencoderが再構成できるデータを生成するので、{\mathcal{L}(G(z))}は小さい。
  • また，kが小さいと、式(3)における{\mathcal{L}(x)}の重要性が増すため、Discriminatorは訓練データの再構成誤差を小さくするよう学習する。

よって、このとき{\mathcal{L}(x) > \mathcal{L}(G(z))}となっているため、 式(5)からkが徐々に大きくなっていく．

{k}が大きくなってくると、式(3)における{\mathcal{L}(G(z_{D}))}の重要性が増す。 そうなるとDiscriminatorはこの{\mathcal{L}(G(z_{D}))}を大きくするよう学習するため、 訓練データと生成データの区別をするような学習が促進される。 一気に学習が進んだときには，今度は式(5)からkが小さくなり調整される．

最終的には，式(3)の{{ \mathcal{L}}_{D} = {\mathcal{L}}(x) - k_{t} \cdot {\mathcal{L}}(G(z_{D})) = 0}となる平衡状態へ達する．

一方，Generatorは，式(4)でひたすら生成データの誤差が小さくなるよう学習する． (Discriminatorからすると，生成データと訓練データの区別が難しくなっていく）

いらすとや画像の生成

このBEGANでいらすとや画像を生成してみた。
結論からいうと、mode collapseしてしまいうまく行かなかった。
かなり綿密なパラメータ調整が必要のよう。

誤差など

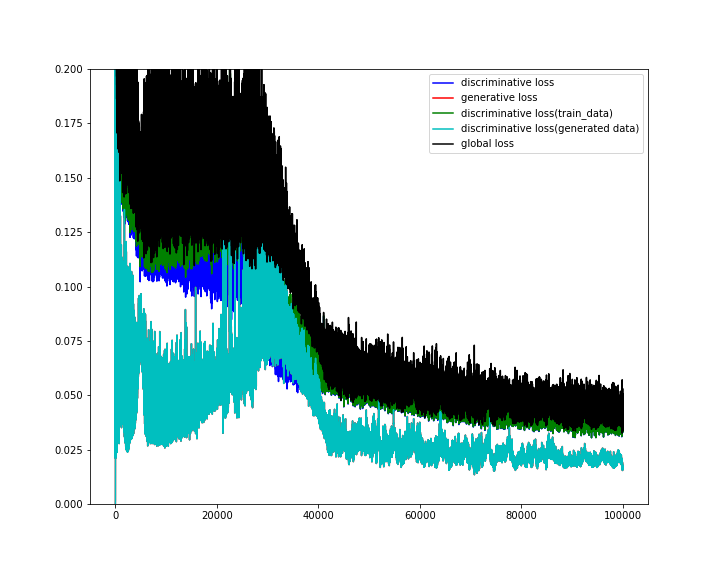f:id:yusuke_ujitoko:20170530010947p:plain mode collapseが起きた40000epochあたりで誤差が激減している。

生成画像

学習開始(0epoch)

f:id:yusuke_ujitoko:20170530005500p:plain

うっすらと何かが見え始める(1000epoch)

f:id:yusuke_ujitoko:20170530005512p:plain

輪郭が現れてくる(5000epoch)

f:id:yusuke_ujitoko:20170530005538p:plain

肌色が付き始める(6000epoch)

f:id:yusuke_ujitoko:20170530005600p:plain ここからしばらく変化なしの状態が続く。

色んなmodeが現れる(33000epoch)

f:id:yusuke_ujitoko:20170530005913p:plain

mode collapse状態になる(45000epoch)

f:id:yusuke_ujitoko:20170530010001p:plain

以降はずっとmode collapseしたまま…(100000epoch)

60000epochあたりから、背景が白固定になる。

f:id:yusuke_ujitoko:20170530010053p:plain

animation(チカチカするので注意)

f:id:yusuke_ujitoko:20170530011340g:plain

BEGANはmode collapseしやすいのがよく分かった。
パラメータ調整は今後も続けて、うまく行ったら追記することとする。