2クラスの線形識別関数を求める古典的な手法に、パーセプトロンの学習規則がある。 識別関数のパラメータを逐次的に求めるこのアルゴリズムは、2クラスの学習データが線形分離可能であれば収束することが知られている。 これをパーセプトロンの収束定理という。
パーセプトロンの学習や誤差逆伝播法などは、 ゼロから作るディープラーニングや深層学習などで散々学んできたので今回はメモしないことにした。
はじめてのパターン認識を読んでいる。
その個人的メモ。

1次元に写像されたとき、クラス間の分布ができるだけ重ならないような写像方向を見つけるのが線形判別分析。
線形識別関数と線形判別関数の違いは、 線形識別関数がクラス分けを目的としているのに対して、線形判別関数はクラス分離をよくすることを目的として考えられていること。
このフィッシャーの線形判別関数の節で少し詰まったので丁寧に書き下していきたい。
フィッシャーの方法の基本的な考え方は、
クラス間変動のクラス内変動に対する比、クラス内変動・クラス間変動比を最大にする一次元軸を求めることにある。
すなわち、変換後の空間において2つのクラスがよく分離するために、変換ベクトルを求めるわけである。
例として、2クラス()の問題について考える。
はクラス
の変換前の平均、
はクラス
のデータサンプル数とする。
ここで変換前のクラス内変動行列とクラス間変動行列
を以下のようにして求める。
$$
\begin{align}
S_{W} &= \sum_{i=1,2} \sum_{x} (x-\mu_{i})(x-\mu_{i})^{t} \\
S_{B} &= \sum_{i=1,2} n_{i} (\mu_{i} - \mu)(\mu_{i} - \mu)^{t} \\
&= \frac{n_{1} n_{2}}{n} (\mu_{1} - \mu_{2})(\mu_{1} - \mu_{2})^{t}
\end{align}
$$
さて、で変換後のクラスの平均を
とすると、
$$
\begin{align}
m_{i} &= \frac{1}{n_{i}} \sum_{y} y \\
&= \frac{1}{n_{i}} \sum_{x} w^{t} x \\
&= w^{t} \mu_{i}
\end{align}
$$
となる。
変換後の空間でのクラス内変動行列
、クラス間変動行列
も同様に求めることができる。
$$
\begin{align}
\tilde{S}_{W} &= \sum_{i=1,2} \sum_{y} (y - \tilde{m}_{i})^{2} \\
&= w^{t} S_{W} w \\
\tilde{S}_{B} &= \sum_{i=1,2} \sum n_{i} (m_{i} - m)^{2} \\
&= \frac{n_{1} n_{2}}{n} (m_{1} - m_{2})^{2} \\
&= w^{t} S_{B} w
\end{align}
$$
上に述べたように、フィッシャーの判別ではクラス内変動とクラス間変動の比が大きくなるように変換を定める。
これを定式化すると、
$$
J(w) = \frac{w^{T} S_{B} w}{w^{T} S_{W} w}
$$
となる。
この式を最大化する解を求める。
そのために
で偏微分すると、
$$
\frac{\partial}{\partial w} \frac{w^{T} S_{B} w}{w^{T} S_{W} w} =
\frac{2}{(w^{T} S_{W} w)^{2}} \left[ (w^{T} S_{W} w) S_{B}w - (w^{T} S_{B} w) S_{W} w \right]
$$
が0になればよいので、満たしておかなければならない条件は、
$$
(w^{T} S_{B} w) S_{W} w = (w^{T} S_{W} w) S_{B}w
$$
となる。
ちなみに、線形変換
は方向のみに興味があるので、大きさの情報に意味はない。
二次形式の部分はスカラー値なので、無視してよい。
すなわち以下のように評価をしても良いということになる。
$$
S_{W} w \propto S_{B} w
$$
両辺に
を左からかけて、
さらに
が
に比例することを用いると、
$$
w \propto S_{W}^{-1} S_{B} w \propto S_{W}^{-1} (m_{1} - m_{2})
$$
となる。これがフィッシャーの基準による最適な
となる。
この意味するところは、結局、
クラスごとの平均の差を求めて、クラス内変動行列
を計算して、
その逆行列を求めれば
は決まるということ。
によって変換された特徴空間は,クラス内変動,クラス間変動比を最大にする一次元空間となる.
線形判別法で注意が必要な点は,線形判別法によって決まるのは空間のみであって,軸上に設けるべき識別のための境界は定まらないという点である.
このような場合に軸上に決定境界を決定する方法は,
などがある.
フィッシャーの方法をより一般的な形で表現するため,
変動行列の代わりに共分散行列と事前確率を用いた定式化を試みる.
クラス
の共分散行列
はクラス
に属するパターンの共分散行列であり,
$$
Σ_{i} = \frac{1}{n_{i}} \sum (x-m_{i}) (x-m_{i})^{t} = \frac{1}{n_{i}} S_{i}
$$
で定義される.
クラス内共分散行列
,クラス間共分散行列
を
$$
\begin{align}
Σ_{W} &= \sum P(C_{i}) Σ_{i} \\
&= \sum ( P(C_{i}) \frac{1}{n_{i}} \sum (x-m_{i}) (x-m_{i})^{t} ) \\
Σ_{B} &= \sum P(C_{i}) (m_{i} - m) (m_{i} - m)^{t} \\
&= P(C_{1}) P(C_{2}) (m_{1} - m_{2}) (m_{1} - m_{2})^{t}
\end{align}
$$
と定義する.
変換行列
によって変換した空間上でも,
,
を求めることができ,
$$
\begin{align}
\tilde{Σ}_{W} &= P(C_{1}) \tilde{σ}_{1}^{2} + P(C_{2}) \tilde{σ}_{2}^{2}
\end{align}
$$
numpy arrayの演算操作についての自分用メモ
numpyにおけるarrayのサイズはなかなか直感的に理解するまで時間がかかると思う。
ベクトルとそれ以外でとりあえず分ければよいのだなと感じた.
import numpy as np a = np.array([1]) a.shape # (1,) b = np.array([1,2]) b.shape # (2,) c = np.array([[1]]) c.shape # (1, 1) d = np.array([[0], [2]]) d.shape # (2, 1)
a = np.zeros((3,7)) at = a.T print(at.shape) # (7, 3)
ただし以下のようにnumpyでは列ベクトルと行ベクトルを意識していない。
そのため、転置はされない。
x = np.zeros(10) xt = x.T print(xt.shape) # (10,)
a = np.array([[1,2],[3,4],[5,6]]) print(a[0]) # [1 2] print(a[::-1]) # [[5 6] # [3 4] # [1 2]] print(a[:,::-1]) # [[2 1] # [4 3] # [6 5]] print(a[::-1, ::-1]) # [[6 5] # [4 3] # [2 1]]
Advanced indexingには2つ種類がある。
抽出する行と列を別々に指定するのがAdvanced indexingと理解
x = np.array([[1,2], [3,4], [5,6]]) print(x) # [[1 2] # [3 4] # [5 6]] print(x[[0,1,2], [0,1,0]]) # [1 4 5] print(x[[0]]) # [[1 2]] print(x[[0,1],[1]]) # [2 4]
x = np.array([1, -1, -2, 3]) print(x[x < 0]) # [-1 -2] x[x<0] += 20 print(x) # [ 1 19 18 3]
# 集約演算 x = np.array([[1,2], [3,4], [5,6]]) print(x) # [[1 2] # [3 4] # [5 6]] print(x.sum()) # 21 print(x.sum(axis=0)) # [0,:]と[1,:]と[2,:]の和 # [ 9 12] print(x.sum(axis=1)) # [:,0]と[:,1]の和 # [ 3 7 11]
もういちどだけ内積・外積 [物理のかぎしっぽ] テンソル積については別にまとめる必要がある。
はじめてのパターン認識を読んでいる。
その個人的メモ。

2クラス問題を考える。
条件付きベイズ誤り率は、事後確率の小さい方
$$
\epsilon (x) = \min{ [ P(C_1|x), P(C_2|x) ]}
$$
である。
ベイズ誤り率は、その期待値が
$$
\epsilon \ast = \int \epsilon (x) p (x) dx
$$
で表される。
入力の最近傍鋳型を
とする。
N個の鋳型の集合をとする。
このとき以下の漸近仮定が成り立てば、
$$
\lim_{N \to \inf} T_{N} \Rightarrow d(x, x_{1NN}) \to 0
$$
kNN誤り率とベイズ誤り率の間には、次の関係が成り立つ。
$$
\frac{1}{2} \epsilon \ast \geq \epsilon_{2NN} \geq \epsilon_{4NN} \geq \cdots \geq \epsilon \ast \geq \cdots \geq \epsilon_{3NN} \geq \epsilon_{1NN} \geq \epsilon_{1NN} \geq 2 \epsilon \ast
$$
教科書にはこの証明が載っていてかなり面白い。
簡単な周期関数をLSTMネットワークに学習させ、予測させてみる。
今回予測させる周期的な関数は、 周期の異なるsinとcosの和で作る。 (下図上段のオレンジと黄の曲線)
この周期関数 は以下の式で表される。
$$
y = \sin(\frac{\pi x}{20}) +
\cos(\frac{\pi 3 x}{20})
$$
(下図中段の赤い曲線)
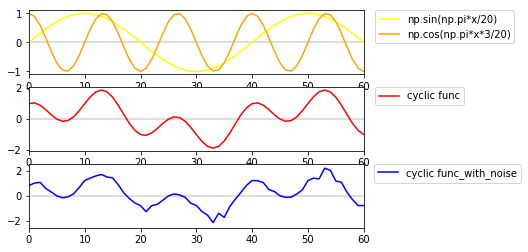
なお、そのまま学習させるとあまりにも簡単なので、
ノイズを混ぜた曲線を学習させることにした。
(上図下段の青い曲線)
from random import random import numpy as np x = np.arange(0, 2000) data = np.sin(np.pi*x/20) + np.cos(np.pi*x*3/20) # 予測させたい周期関数 data_noised = [d * (0.75+0.5*random()) for d in data] # ノイズを混ぜる
イメージとしては、過去の時刻から現在までの全てのデータを入力したら、 現在の1つ先のデータが出力される感じ。
from keras.models import Sequential from keras.layers.core import Dense, Activation from keras.layers.recurrent import LSTM in_out_neurons = 1 hidden_neurons = 30 model = Sequential() model.add(LSTM(hidden_neurons, return_sequences=False, input_shape=(None, in_out_neurons))) model.add(Dense(in_out_neurons, input_dim=hidden_neurons)) model.add(Activation("linear")) model.compile(loss="mean_squared_error", optimizer="rmsprop")
________________________________________________________________ Layer (type) Output Shape Param # ================================================================= lstm_18 (LSTM) (None, 30) 3840 _________________________________________________________________ dense_18 (Dense) (None, 1) 31 _________________________________________________________________ activation_18 (Activation) (None, 1) 0 ================================================================= Total params: 3,871.0 Trainable params: 3,871.0 Non-trainable params: 0.0 _____________________________
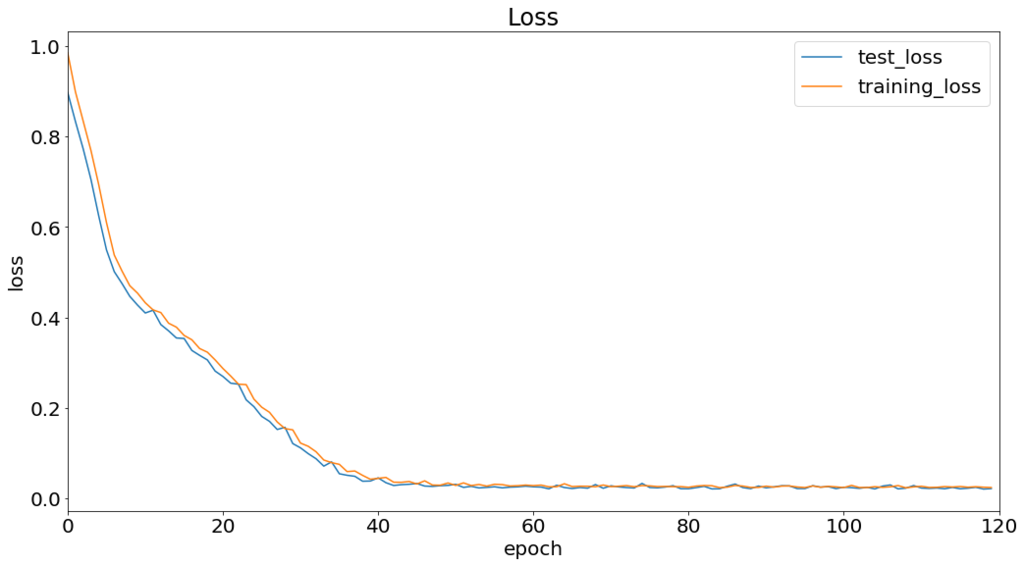
60epoch程度で収束している。
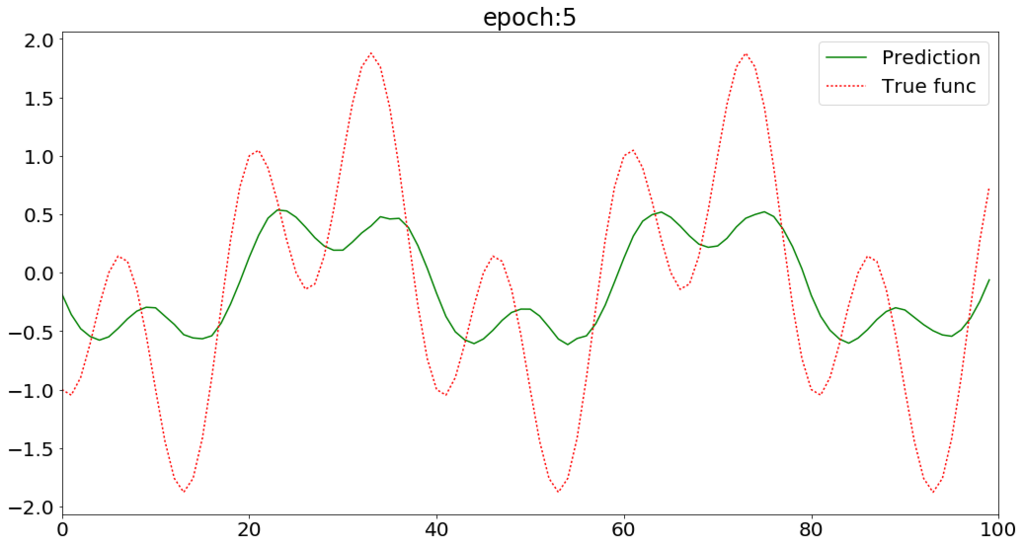
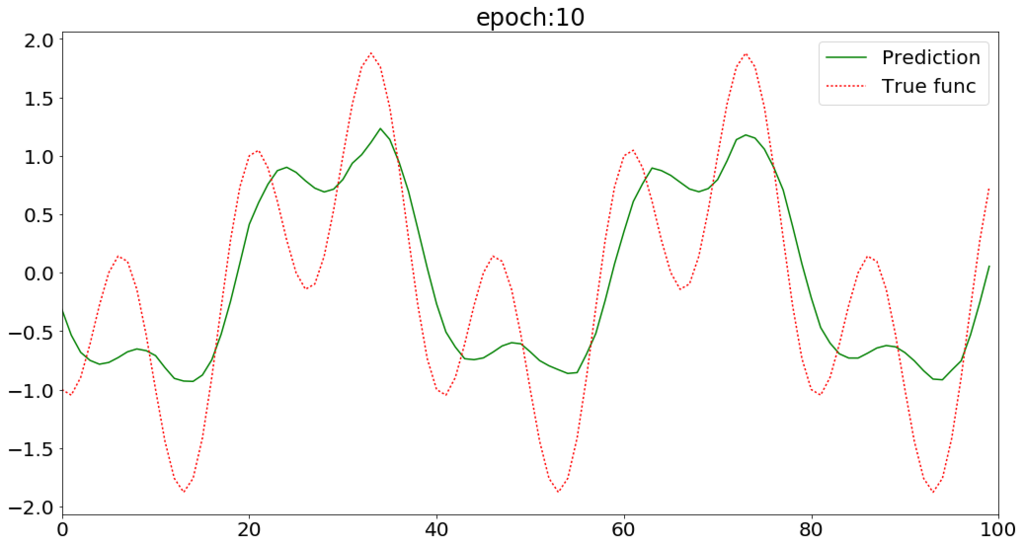
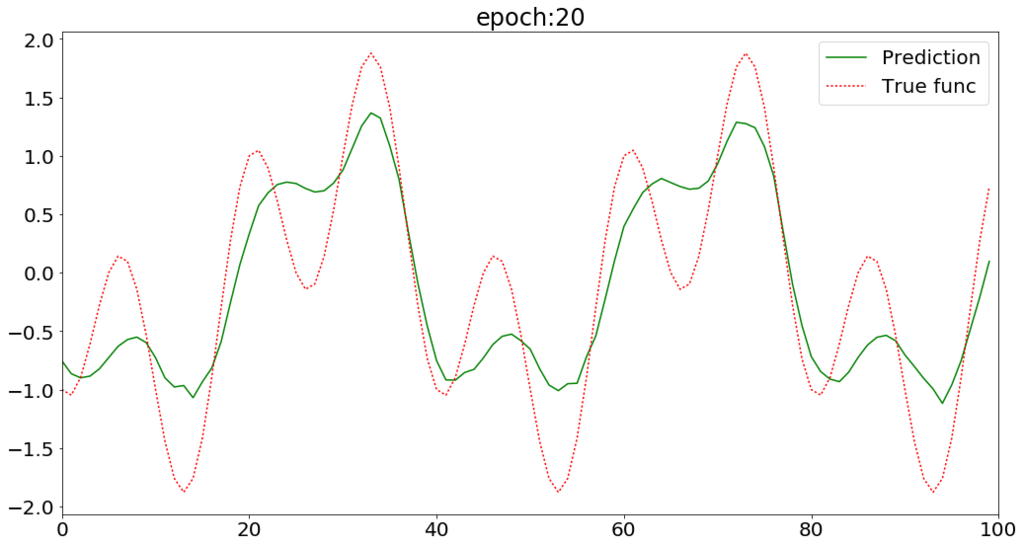
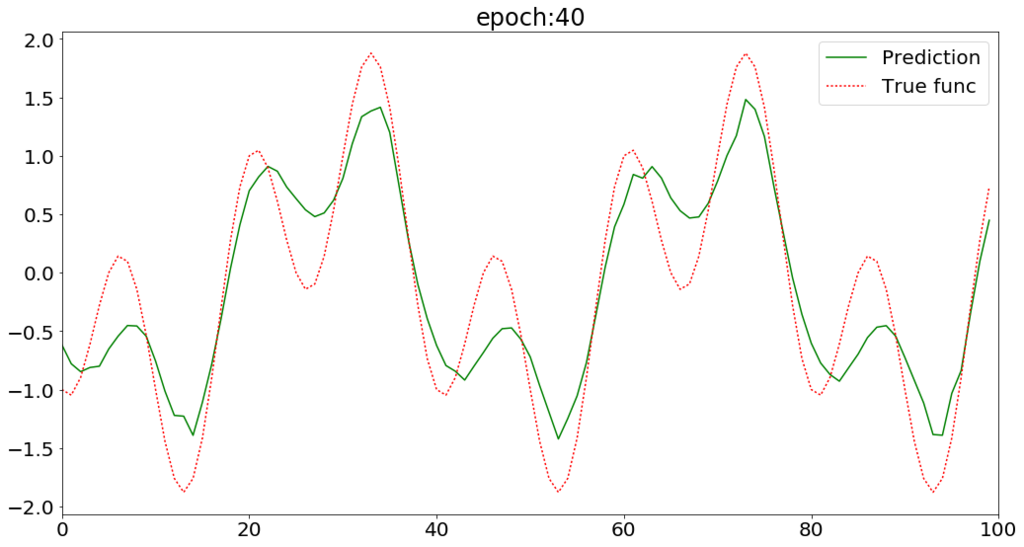
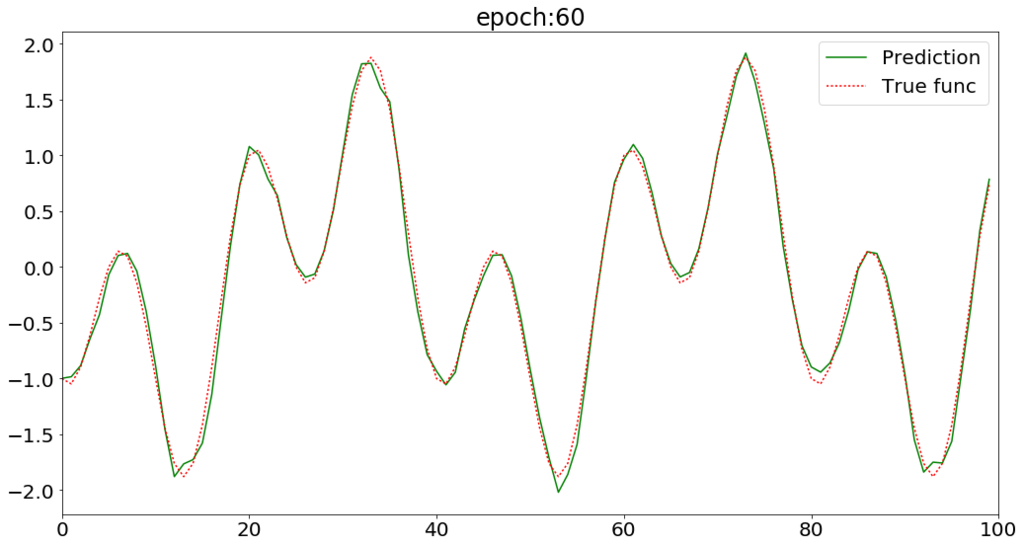
LSTMで周期関数の予測ができた。 次はもう少し複雑な系列データを予測してみたい。