誤差逆伝播法の数式を簡単なニューラルネットで理解する

誤差逆伝播法の数式をニューラルネットで追ってみる。
時々忘れてしまうので、備忘録として残しておく。

今回考えるニューラルネット

下記のニューラルネットを例に取る。 層への入力を、
層のアクティべーションを、
層から層への重みをとしている。 なお入力層は活性化しない。
この時、各層間の結合は下記の式のようになる。 $$ \left\{ \begin{array}{} u_4 = w_3 a_3 \\ u_3 = w_2 a_2 \\ u_2 = w_1 u_1 \\ \end{array} \right. $$ 上記の式を、や、について偏微分した下記の式も成り立つ。 $$ \left\{ \begin{array}{} \frac{\partial u_4}{\partial w_3} = a_3 \\ \frac{\partial u_3}{\partial w_2} = a_2 \\ \frac{\partial u_2}{\partial w_1} = a_1 \\ \end{array} \right. \\ \left\{ \begin{array}{} \frac{\partial u_4}{\partial a_3} = w_3 \\ \frac{\partial u_3}{\partial a_2} = w_2 \\ \frac{\partial u_2}{\partial a_1} = w_1 \\ \end{array} \right. $$

また活性化関数をとすると、下記の関係式が成り立つ。 $$ \left\{ \begin{array}{} a_4 = f(u_4) \\ a_3 = f(u_3) \\ a_2 = f(u_2) \\ \end{array} \right. $$ 上記をで偏微分した式も記しておく。 $$ \left\{ \begin{array}{} \frac{\partial a_4}{\partial u_4} = f'(u_4) \\ \frac{\partial a_3}{\partial u_3} = f'(u_3) \\ \frac{\partial a_2}{\partial u_2} = f'(u_2) \\ \end{array} \right. $$

誤差逆伝播法

誤差をとする。
また、は既知とする。

を求める。

連鎖律を利用すると、下記となる。 $$ \begin{align} \frac{\partial E}{\partial u_4} &= \frac{\partial E}{\partial a_4} \frac{\partial a_4}{\partial u_4} \\ &= \frac{\partial E}{\partial a_4} f'(u_4) \end{align} $$ この式は、誤差の出力に対する偏微分が、誤差のアクティベーションに対する偏微分に、活性化関数の微分 を掛けたものであることを示している。

を求める

次は、を求める。

連鎖律を利用すると、下記のようになる。 $$ \begin{align} \frac{\partial E}{\partial w_3} &= \frac{\partial E}{\partial u_4} \frac{\partial u_4}{\partial w_3} \\ &= \frac{\partial E}{\partial u_4} a_3 \\ &= \frac{\partial E}{\partial a_4} f'(u_4) a_3 \end{align} $$

を求める

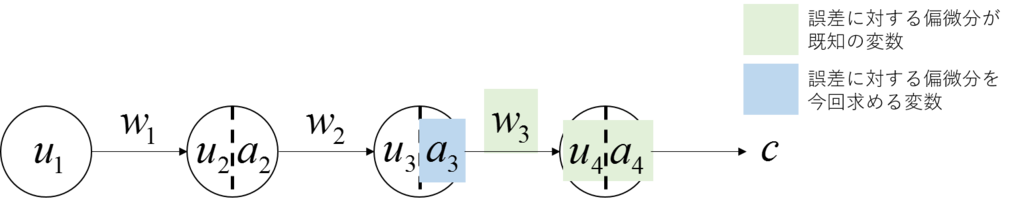次は、を求めるが、これも上記とほぼ同じ導き方ができる。 $$ \begin{align} \frac{\partial E}{\partial a_3} &= \frac{\partial E}{\partial u_4} \frac{\partial u_4}{\partial a_3} \\ &= \frac{\partial E}{\partial u_4} w_3 \\ &= \frac{\partial E}{\partial a_4} f'(u_4) w_3 \end{align} $$

これ以降は繰り返しになる。

、、、、、を求める。

これまでと同様に、連鎖律を使って順番に求められる。 $$ \begin{align} \frac{\partial E}{\partial u_3} &= \frac{\partial E}{\partial a_4} f'(u_4) w_3 f'(u_3) \\ \frac{\partial E}{\partial w_2} &= \frac{\partial E}{\partial a_4} f'(u_4) w_3 f'(u_3) a_2 \\ \frac{\partial E}{\partial a_2} &= \frac{\partial E}{\partial a_4} f'(u_4) w_3 f'(u_3) w_2 \\ \frac{\partial E}{\partial u_2} &= \frac{\partial E}{\partial a_4} f'(u_4) w_3 f'(u_3) w_2 f'(u_2) \\ \frac{\partial E}{\partial w_2} &= \frac{\partial E}{\partial a_4} f'(u_4) w_3 f'(u_3) w_2 f'(u_2) u_1 \\ \frac{\partial E}{\partial u_1} &= \frac{\partial E}{\partial a_4} f'(u_4) w_3 f'(u_3) w_2 f'(u_2) w_1 \\ \end{align} $$

勾配消失や勾配爆発の原因

上式を見ると、前方の層になるにつれて、活性化関数の導関数や重みが繰り返し掛け合わされているのがわかる。
活性化関数を例えばシグモイドと設定すると、シグモイドの導関数の最大値は1/4であるので、 そのシグモイドンホ導関数が繰り返し掛けられると、勾配が徐々に小さくなっていってしまう。
これが勾配消失問題である。

一方、重みが大きい値を取ると、 前方の層に伝わるに際に、その重みが影響して勾配が大きくなる。
そうなると勾配が不安定となる。
これが勾配爆発問題である（と私は理解している）。

参考

ニューラルネットワークと深層学習