- Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
- arXiv:https://arxiv.org/abs/1502.03167
Internal Covariance Shiftの問題
ニューラルネットワークでは,入力となるデータの分布が白色化されていると学習が早く進む. 特徴を無相関化し,平均0,分散1とすることは画像処理では特によく行う.
しかし,階層的なニューラルネットでは,入力層での入力データが白色化されていたとしても,
重みパラメータは更新されていくため,後層では常に分布が変化する入力をもとに学習することになる.
せっかくパラメータを学習しても、新たな入力分布に合わせて再適応させなければならず、無駄となってしまう。
この現象を著者らは, internal covariance shift と呼んでいる.
分布をコントロールしないこのような場合には、勾配消失問題も起きやすくなる。
このときには,
- 学習率を小さく設定する
- 重みの初期化を注意深く行う
などの処置を行う必要がある。
そこでこの論文では上記の問題を回避する、Batch Normalizationを提案している。
Batch Normalizationでは以下のように,
ミニバッチ内で平均を0に,分散を1にする操作を行う.

上図の最後の行を見ると, gamma と beta を掛けて細かい調整ができるようになっている. たとえば,Batch Normalizationの効果をキャンセルすることもできる (gamma を標準偏差に設定し,betaを平均に設定する)
ただし,このgammaとbetaは学習できるパラメータとなっているため, 人が自由に決められる訳ではない. 単純に表現力を増やした,という意味と解釈した.
BatchNormalizationには、
- ミニバッチ単位で平均・分散を正規化するため計算量が小さい
- ミニバッチ単位で微分可能
という特徴がある。 アルゴリズムはどのようになるかというと
訓練時はミニバッチごとに正規化し、
一方、テスト(inference)時は、全訓練データから学習した情報で正規化したいため、
分散は訓練データの平均、不偏分散を使う。
どこにBatch Norm層を挿入するかというと, 普通は全結合層や畳み込み層の直後で,活性化関数の直前.
MNISTの結果
論文の図をそのままのせる。
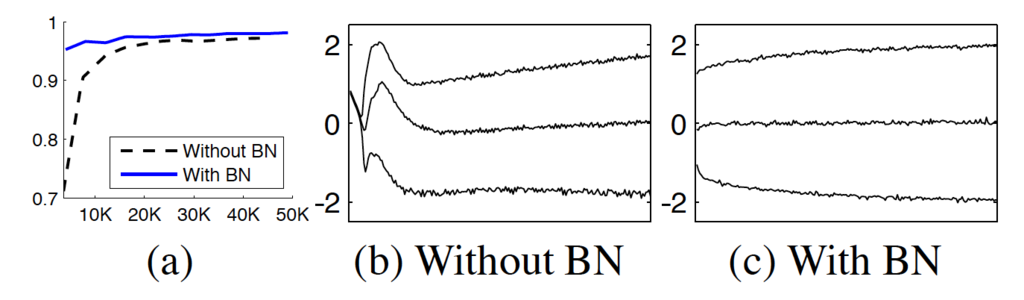
収束が早く、また入力分布は安定しているのがわかる。
読み解けなかった点
regularizationの意味
Batch Normによる正則化の効果を謳う文句がところどころに散見されるが, その正則化の意味がよくわからなかった.
Furthermore, batch normalization regularizes the model and reduces the need for Dropout (Srivastava et al., 2014).
When training with Batch Normalization, a training example is seen in conjunction with other examples in the mini-batch, and the training network no longer producing deterministic values for a given training example.
バッチに含まれる訓練データに依存して各データは正規化されるが, そのバッチの選び方はdeterministicでないため,結果的に訓練データの正規化のされ方もdeterministicではなく, ばらつきがあるので,訓練データの拡張につながって,正則化の効果があるという意味?
Reduce the photometric distortions.の意味
Batch Normのネットワークにおけるテクニックの最後の例として, Reduce the photometric distortionsが紹介されているが, これは訓練データの拡張をあまりしない,という意味?
Because batchnormalized networks train faster and observe each training example fewer times, we let the trainer focus on more “real” images by distorting them less.
(追記)計算グラフによる誤差逆伝播
以下のブログで, 計算グラフで誤差逆伝播を丁寧に解説してある.
Understanding the backward pass through Batch Normalization Layer