【Deep Learning】計算グラフによる誤差逆伝播法（Back propagation）の理解

背景

ニューラルネットの重みなどのパラメータ決定を勾配法で行う
勾配法の計算の際に損失関数の微分が必要
微分計算の高速化が求められる．
その高速化のために誤差逆伝播法を用いるのが一般的
その誤差逆伝播法を数式ではなく，計算グラフから理解してみる．

計算グラフとは

複雑な処理からなる計算を可視化する方法として，計算グラフ（Computational graph）がある．

例えば， ${e = (a + b)*(b + 1)}$ という数式を考える．
3つの演算からなり，加算が2つで乗算が1つ．
この式を計算グラフ化すると下図のようになる．

f:id:yusuke_ujitoko:20161231102417p:plain:w500

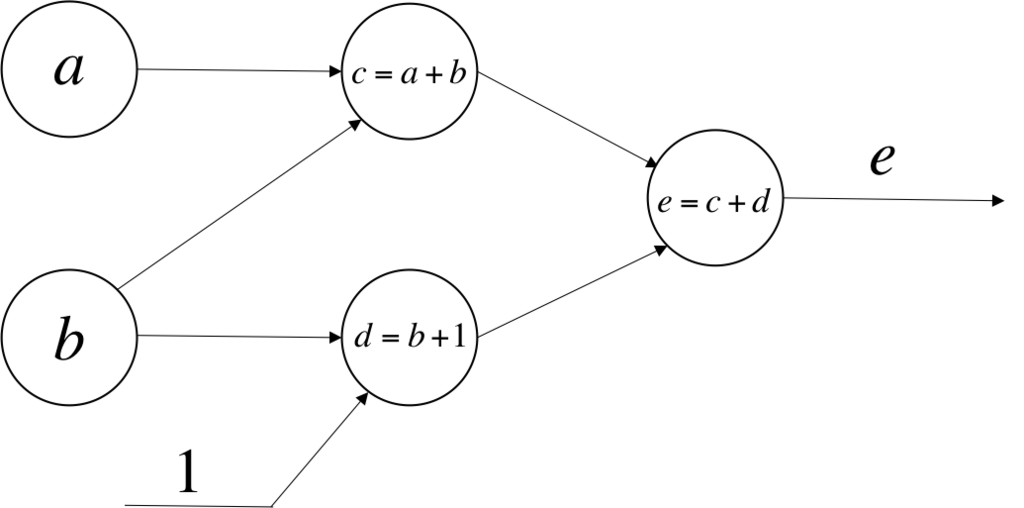
この式の値をもとめるには，入力変数に特定の値を代入して，ノードを順に計算していく．
たとえば， ${a = 2}$ ， ${b = 3}$ とすると，式の値は20になる．

f:id:yusuke_ujitoko:20161231102756p:plain:w500

計算グラフの自動微分

アルゴリズムで定義された関数を解析し，微分を計算するアルゴリズムを導出する技術のことを自動微分（Automatic differentiation）という．

計算グラフを使ってその自動微分を計算してみよう．
たとえば上図で，a方向のeの微分や，b方向のeの微分は何だろう．

計算グラフを見ると，直接接続されているノード間では，微分を計算できそうだ．
たとえば，a方向のcの微分や，b方向のcの微分などだ．
これらを図に加えると以下のようになる．

f:id:yusuke_ujitoko:20161231225452p:plain:w500

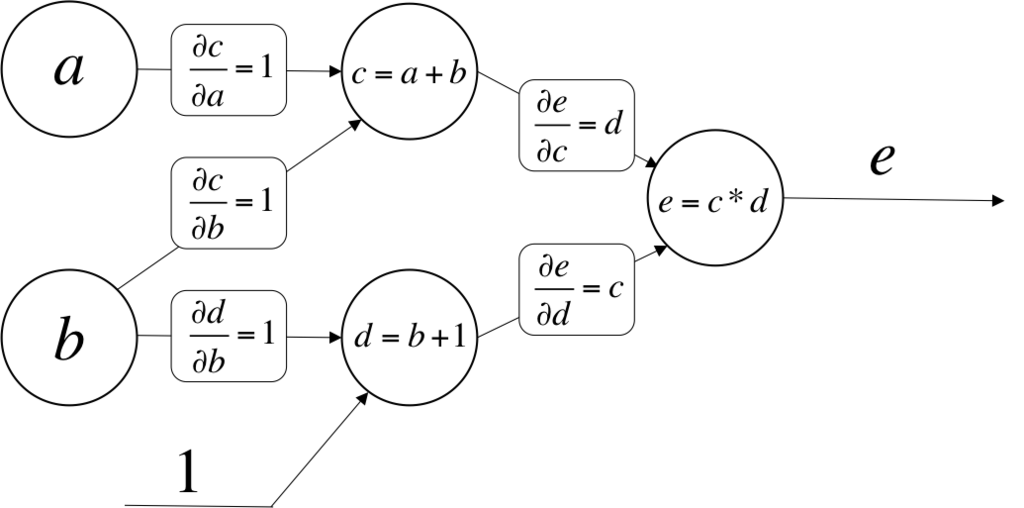
では，直接接続されていないノード間の微分はどう求めるのか？
たとえばaはどうeに影響するのかを追ってみると，
aは1変化したら，上図からcは1変化する．
cが1変化すると，上図からeはd変化する．
結果的に，aが1変化するとeはd変化することになる．

あるノードからあるノードへの微分を求めるときには，道筋の微分係数を合計する．
例えばbに対するeの微分係数は，b→c→eとb→d→eの2つの道筋を考えて， ${}$ $$ \frac{\partial e}{\partial b} = 1 * d + 1 * e $$ となる．

この方法は直観的であり，自動微分の中でもforward-modeと呼ばれる方法だ．
でもニューラルネットの場合，後述するreverse-modeの方が適している．

forward-mode自動微分とreverse-mode自動微分

計算グラフから微分を導く方法には2種類ある．
forward-mode とreverse-modeだ．

どちらも基本原理は連鎖律を用いた微分の分解である．
たとえば，シンプルな合成関数である ${ y = g(h(x)) = g(w) }$ に対して連鎖律を適用すると，以下を得る． ${}$ $$ \frac{dy}{dx} = \frac{dy}{dw} \frac{dw}{dx} $$

forward-modeは連鎖律を内側から外側に計算し，
reverse-modeは連鎖律を外側から内側に計算する．

forward-mode自動微分

forward-modeでは，最初に微分を行う入力変数を決めて，全ての中間変数の微分を計算していく．

下図の ${a}$ ， ${b}$ ， ${c}$ ， ${d}$ ， ${e}$ の5つの変数の入力変数 ${b}$ に対する微分を計算すると，

以下のようになる．

f:id:yusuke_ujitoko:20161231234352p:plain:w500

${ \frac{\partial a}{\partial b} = 0 }$
${ \frac{\partial b}{\partial b} = 1 }$
${ \frac{\partial c}{\partial b} = \frac{\partial (a + b)}{\partial b} = 1 }$
${ \frac{\partial d}{\partial b} = \frac{\partial (b + 1)}{\partial b} = 1 }$
${ \frac{\partial e}{\partial b} = \frac{\partial (c \cdot d)}{\partial b} = \frac{\partial c}{\partial b} \cdot d + c \cdot \frac{\partial e}{\partial b} = d + c }$

${\frac{\partial e}{\partial e}}$ の計算をするときに，既に算出した下流の ${\frac{\partial e}{\partial c}}$ ， ${\frac{\partial e}{\partial d}}$ を利用している．

このように，下流の計算で上流の結果を利用するのが，forward-modeの特徴となる．
出力変数が多いときにはこのforward-modeを使うのが計算量で有利．

reverse-mode自動微分

reverse-modeでは，1つの出力変数について，全ての中間変数に対する微分を計算していく．
例を考えてみる．
出力変数のeについて，各中間変数に対する微分を計算してみる．
reverse-modeでは計算グラフの後ろ側から計算していくイメージだ．

f:id:yusuke_ujitoko:20161231234829p:plain:w500

${ \frac{\partial e}{\partial e} = 1 }$
${ \frac{\partial e}{\partial d} = c }$
${ \frac{\partial e}{\partial c} = d }$
${ \frac{\partial e}{\partial b} = \frac{\partial e}{\partial d} \frac{\partial d}{\partial b} + \frac{\partial e}{\partial c} \frac{\partial c}{\partial b}= c \cdot \frac{\partial (b + 1)}{\partial b} + d \cdot \frac{\partial (a + b)}{\partial b}= c + d }$
${ \frac{\partial e}{\partial a} = \frac{\partial e}{\partial c} \frac{\partial c}{\partial a} = d \cdot \frac{\partial (a + b)}{\partial a} = d }$

${\frac{\partial e}{\partial a}}$ ， ${\frac{\partial e}{\partial b}}$ の計算をするときに，既に算出した下流の ${\frac{\partial e}{\partial c}}$ ， ${\frac{\partial e}{\partial d}}$ を利用している．