【データ解析のための統計モデリング入門】5章 GLMの尤度比検定と検定の非対称性

データ解析のための統計モデリング入門を読んでいる。
その読書メモ。

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)

作者: 久保拓弥
出版社/メーカー: 岩波書店
発売日: 2012/05/19
メディア: 単行本
購入: 16人クリック: 163回
この商品を含むブログ (29件) を見る

この章では、どのような統計モデルでも利用可能な尤度比検定(likelihood ratio test)について説明する。
これは前のモデル選択の章に登場した逸脱度の差に注目する考え方。

パラメトリックとノンパラメトリック

全パラメータを最尤推定できる統計モデルは、パラメトリックな統計モデルと総称できる。
ここでいうパラメトリックとは、比較的少数のパラメータをもつという意味。

ノンパラメトリックは、順序統計量を使った、という意味や、多数のパラメータを使って自由自在な構造をもつ、といった意味にも使われる。

統計学的な検定の枠組み

尤度比検定の例題：逸脱度の差を調べる

今回の例題では以前扱った、単純モデル・複雑モデルをそれぞれ帰無仮説・対立仮説とする。
尤度比検定では最大尤度の比を扱う。
${}$ $$ \frac{L_1}{L_2} = \frac{一定モデルの最大尤度}{xモデルの最大尤度} $$

しかしこれをそのまま検定統計量として使うわけではない。
尤度比検定では、尤度比の対数を取り、-2をかける。
つまり逸脱度の差に変換して検定統計量として使う。
${}$ $$ ΔD_{1,2} = −2 \times (Log L_{1} – Log L_{2}) $$

例題では逸脱度の差は4.5程度だった。
尤度比検定では、逸脱度の差がこの4.5程度で改善されているとみなすのかを調べる。

検定全体のステップとしては以下のようになる。

まずは帰無仮説である一定モデルが正しいものだと仮定する
観測データに一定モデルを当てはめると、 ${\beta_1 = 2.06}$ となったので、これは真のモデルとほぼ同じと考えよう
この真のモデルからデータを何度も生成し、そのたびに ${\beta_2 = 0}$ と ${\beta_2 ≠ 0}$ のモデルを当てはめれば、沢山の ${⊿D_{1,2}}$ が得られるから、 ${⊿D_{1,2}}$ の分布がわかるだろう。
そうすれば、一定モデルとxモデルの逸脱度の差が ${⊿D_{1,2} > 4.5}$ となる確率Pが評価できるだろう。

汎用性のあるパラメトリックブートストラップ法

パラメトリックブートストラップ法は、データを何度も生成する過程を乱数発生のシミュレーションによって実施する方法。

まず一定モデルとxモデルの逸脱度の差を計算する。

import statsmodels.api as sm
import statsmodels.formula.api as smf

fit1 = smf.glm(formula='y ~ 1', data=df, family=sm.families.Poisson())
fit2 = smf.glm(formula='y ~ x', data=df, family=sm.families.Poisson())

# 逸脱度の差
print(fit1.fit().deviance - fit2.fit().deviance)

4.51394107885

一定モデルを真のモデルとして、ここから100個新たにデータを生成し、一定モデルとxモデルをこの新データに当てはめる。

df['y_rnd'] = np.random.poisson(df.y.mean(), 100)

fit1 = smf.glm(formula='y_rnd ~ 1', data=df, family=sm.families.Poisson())
fit2 = smf.glm(formula='y_rnd ~ x', data=df, family=sm.families.Poisson())

# 逸脱度の差
print(fit1.fit().deviance - fit2.fit().deviance)

0.00103719102299

こうして一定モデルを真のモデルと仮定したもとでの逸脱度を繰り返し貯めていく。

def get_dd(df):
    df['y_rnd'] = np.random.poisson(df.y.mean(), 100)

    fit1 = smf.glm(formula='y_rnd ~ 1', data=df, family=sm.families.Poisson())
    fit2 = smf.glm(formula='y_rnd ~ x', data=df, family=sm.families.Poisson())

    # 逸脱度の差
    return (fit1.fit().deviance - fit2.fit().deviance)

def pb(df, n_bootstrap):
    return pd.Series([get_dd(df) for i in range(n_bootstrap)])

dd12 = pb(df, 1000)
print(dd12.describe())

こうして得た逸脱度を視覚化する。

plt.hist(dd12, 100)
plt.xlim(0, 14)
plt.axvline(x=4.5, linestyle='--')

plt.savefig("hst.png")

f:id:yusuke_ujitoko:20170312184317p:plain

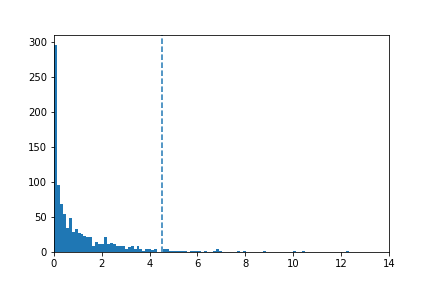
この逸脱度の集合のうち、4.5より右にある数は

print(sum(dd12 >= 4.5))

37個となった。
つまりp=37/1000=0.037ということになる。
よってP値が0.037だったので、これは有意水準0.05よりも小さいので有意差ありと判断され、帰無仮説は棄却される。

χ二乗分布を使った近似計算法

逸脱度の差の確率分布は、自由度1の[tex:{\chi²}]分布で近似できる場合がある。

まとめ

Neyman-Pearsonの統計学的検定の枠組みでは、パラメータ数の少ないモデルを帰無仮説と位置づけ、帰無仮説が棄却できるかの確率評価に専念する
尤度比検定の検定統計量はふたつの統計モデルの逸脱度差である
検定における過誤は2種類あるが、Neyman-Pearsonの検定の枠組みでは帰無仮説の誤棄却を重視する
帰無仮説を棄却する有意水準αの大きさは解析者が任意に決めるものである。
Neyman-Pearsonの検定の枠組みでは、第一種の過誤の大きさを正確に評価できるが、一方で帰無仮説が棄却できない場合の結論は何もいえない。判断を保留する。
検定やモデル選択の結果だけに注目するのではなく、推定された統計モデルが対象となる現象の挙動を、どのように予測しているのかも確認するべきだ。

yusuke-ujitoko.hatenablog.com