Generative Adversarial Nets(GAN)はニューラルネットワークの応用として、結構な人気がある。たとえばYann LeCun(現在はFacebookにいる)はGANについて以下のように述べている。
“Generative Adversarial Networks is the most interesting idea in the last ten years in machine learning.”
GANを始めとする生成モデル系研究は、 これまで人間にしかできないと思われていたクリエイティブな仕事に対して、 機械学習が踏み込んでいく構図なためか、個人的にもワクワクする分野だ。
これまで分類問題を中心に実装してきてそろそろ飽きてきたため, 一番最初のGAN論文を頑張って理解して、 その内容をkerasで実装してみることにする.
Generative Adversarial Networks(GAN)のざっくりした紹介
GANでは2つのモデルを競合するように学習させていく. これら2つの関係は,貨幣の偽造者(counterfeiter)と,それを見抜く警察(police)によく例えられる.
偽造者の目的は,本物に似せた偽貨幣を作って警察を欺くことである. 一方,警察の目的は,真の貨幣と偽貨幣の集合から真の貨幣のみ区別することである. この対立する目的を持つモデル同士を競わせるプロセスのため,Adversarial(敵対的) Processと呼ばれる.
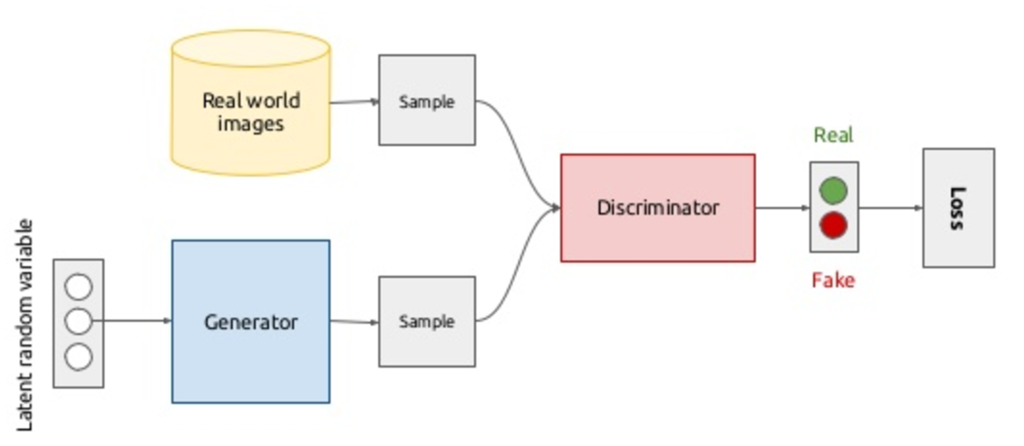
GANでは全体のネットワークの中に,警察と偽造者のネットワークが組み込まれる形になっている.
 (source)
(source)
ここでは,偽造者のネットワークを (Generator)とする。
一方,警察のネットワークを
(Discriminator)とする.
Generator は画像を生成する.
どのように生成するかというと,一様分布や正規分布などからサンプリングしたノイズベクトル
をアップサンプリングして画像とする.
一方,Discriminator は単純な分類問題を解くものとなっており,
Generator
の生成した画像と,本物の画像を分類する.
この2つのネットワークを交互に学習していけば、Generatorは本物のデータに近いデータを生成するようになる。 …というのがGANのおおざっぱな枠組み。 たしかにネットワークを実装すればそのままうまく行くようだが、 イマイチこれでいいのか納得感が薄いので、もう少し詳細に見ていきたい。
Discriminatorによる密度比推定
本物のデータとGeneratorの生成したデータの条件付き分布は次のようになる。
$$
p(x \mid y) =
\left\{
\begin{array}{}
p_{g}(x) & (y = 0) \\
p_{delta}(x) & (y = 1)
\end{array}
\right.
$$
簡単のためとする。
このとき
と
の密度比は、ベイズの定理より、
$$
\frac{p_{delta}(x)}{p_{g}(x)} = \frac{p(x \mid y=1)}{p(x \mid y=0)} = \frac{p(y=1 \mid x)p(y=0)}{p(y=0 \mid x)p(y=1)} = \frac{p(y=1 \mid x)}{p(y=0 \mid x)}
$$
となる。
つまり、識別モデル さえ学習できれば、密度比は推定できるということがわかった。
この密度比が推定できると、divergenceが推定できる。
JS divergence
本物のデータの確率密度関数とGeneratorの生成したデータの確率密度関数
のJS divergenceは以下のように表される。
(JS divergenceについては予め勉強しておいた)
$$
\begin{align}
2D_{JS} &= D_{KL} (p_{delta} (x) \mid \mid \overline{p}(x)) + (p_{g}(x) \mid \mid \overline{p}(x)) \\
&= \mathbb{E}_{p_{delta}(x)} log \frac{2p_{delta}(x)}{p_{delta} (x) + p_{g}(x)} + \mathbb{E}_{p_{g}(x)} log \frac{2p_{g}(x)}{p_{delta} (x) + p_{g}(x)} \\
&= \mathbb{E}_{p_{delta}(x)} log D(x) + \mathbb{E}_{p_{g}(x)} log (1-D(x)) + log4
\end{align}
$$
Discriminatorは、このJS divergenceが大きくなるように学習する。 このときの目的関数は交差エントロピーとなる。 実は私は最初、JS divergenceの式と交差エントロピーが結びつかなくて悩んだ。 結局交差エントロピーを復習したら理解できたので、少しここに示しておく。(若干脱線になるが)
交差エントロピー
n次元ベクトルを2クラスに分類する関数 を考える。
この
が何を示しているかというと、
となるベクトルが1つ目のクラスである確率を示していることになる。
一方、このベクトルが2つ目のクラスである確率を得るには
とすればよい。
このために、
の出力は
の範囲になくてはならない。
そのためには出力層の直前でsigmoidを掛けるなどすればよい。
さらに、
を入力と教師データのペアとしておく。
2つの分布の交差エントロピーは以下のように表される。
$$
H(p,q) = - \sum_{i} p_{i} log q_{i}
$$
と
はそれぞれ真の分布と推定された分布を表す。
この交差エントロピーを誤差関数に適用するために、
真の分布を以下のように定義する。
$$
y_{i} = 0 のとき \mathbb{P} (y_{i}=0) = 1 \\
y_{i} = 1 のとき \mathbb{P} (y_{i}=1) = 1
$$
このとき、ある入力 と教師データに関して、
次の誤差関数を得る。
$$
H([x_{1}, y_{1}], D) = -y_{1} log D(x_{1}) - (1-y_{1}) log(1-D(x_{1}))
$$
注意が必要なのは、上式では、の値により二項のうち一項は必ず0になって消えることだ。
上式はある1つの入力に関するものなので、これをデータセット全体に適用すると、
$$
H([x_{i}, y_{i}]_{i=1}^{N}, D) = - \sum_{i=1}^{N} y_{i} log D(x_{i}) - \sum_{i=1}^{N} (1-y_{1}) log(1-D(x_{1}))
$$
となる。
GANの場合について考える。
GANでは
は二箇所のソースから同数発生している。
すなわち真のデータの確率分布
に従っているか、もしくは生成されたデータの確率分布
に従っているかだ。
どちらの確率分布に由来するかの事前確率は1/2だ。
真のデータに由来するデータの教師データをとすると、
真のデータの場合一項目のみ意味をなす。
逆に生成データは二項目のみ意味をなす。したがって二項目の
は
に置き換えられる。
さらに総和を期待値に置き換え、は定数となるのでとりあえず1で置き換えると、
以下のようになる。
$$
H([x_{i}, y_{i}]_{i=1}^{N}, D) = \mathbb{E}_{p_{delta}(x)} log D(x) + \mathbb{E}_{p_{g}} log (1-D(G(z; \theta_{g})))
$$
これは上の節のJS divergenceの式に等しい。
交差エントロピーの式を変形してJS divergenceの式にできたので、
逆にJS divergenceを最大化するDiscriminatorの目的関数は交差エントロピーでよい。ということになる(と思う)
ちなみのこのDiscriminatorの交差エントロピーは明らかに以下の時に最大になる。
$$
D^{*}(x) = \frac{p_{delta}}{p_{delta} + p_{g}}
$$
一方、GeneratorとしてはこのJS divergenceが小さくなることが望ましい。 実際には、Discriminatorによって最大化された後のJS divergenceを最小化するように学習するのではと考える。
パラメータの更新式
パラメータ、
の更新式は以下のようになる。
$$
\begin{align}
\theta_{d} &\gets \theta_{d} + η \nabla_{\theta_{d}} [\mathbb{E}_{p_{delta}(x)} log D(x) + \mathbb{E}_{p_{g}} log (1-D(G(z; \theta_{g})))] \\
\theta_{g} &\gets \theta_{g} + η \nabla_{\theta_{g}} \mathbb{E}_{p_{g}} log (1-D(G(z; \theta_{g})))]
\end{align}
$$
論文にはこの更新式ではうまくいかないと書いてある。 NIPS2016のTutorial資料にも同様の内容が記述されている。
In the minimax game, the discriminator minimizes a cross-entropy, but the generator maximizes the same cross-entropy. This is unfortunate for the generator, because when the discriminator successfully rejects generator samples with high confidence, the generator’s gradient vanishes.
交差エントロピーによりDiscriminatorの学習が早く進んでしまうため、の値が小さくなり、Generatorの勾配が小さくなり学習が進まなくなる。
よってGeneratorの学習は下のような更新式のようにして、logD(G(z))を最大化するように行う。
$$
\theta_{g} \gets \theta_{g} + η \nabla_{\theta_{g}} \mathbb{E}_{p_{g}} log D ( G ( z; \theta_{g}))
$$
ただ上記のテクニックは理論的に正しいわけではなく、小手先のトリックに過ぎないらしい。 下の実装はもともとの交差エントロピーでGeneratorも学習させている。
GANの実装
,
をそれぞれミニバッチ学習させる.
この表には,kステップ分
を学習させて,1ステップ分
を学習させる.そのkは任意だが,論文ではk=1を使ったと書いてあった.(kと置いた意味はあったのか?)
論文には(なぜか?)構造が載っていなかった。 他の実装を参考にして,モデルの構造は以下のようなものとした.
def Generator(): act = keras.layers.advanced_activations.LeakyReLU(alpha=0.2) Gen = Sequential() Gen.add(Dense(input_dim=100, units=256, kernel_regularizer=l1_l2(1e-5, 1e-5))) Gen.add(BatchNormalization(mode=0)) Gen.add(act) Gen.add(Dense(units=512, kernel_regularizer=l1_l2(1e-5, 1e-5))) Gen.add(BatchNormalization(mode=0)) Gen.add(act) Gen.add(Dense(units=1024, kernel_regularizer=l1_l2(1e-5, 1e-5))) Gen.add(BatchNormalization(mode=0)) Gen.add(act) Gen.add(Dense(units=28*28, kernel_regularizer=l1_l2(1e-5, 1e-5))) Gen.add(BatchNormalization(mode=0)) Gen.add(Activation("sigmoid")) generator_optimizer = SGD(lr=0.1, momentum=0.3, decay=1e-5) # Generatorは単独で訓練しないので下のcompileはいらない Gen.compile(loss="binary_crossentropy", optimizer=generator_optimizer) return Gen
もともとBatchNormalizationを入れていなかった。 何度試しても、異なるノイズをもとに生成しているにも関わらず、同じ一様な画像となってしまうという問題が発生しており、 層がそこそこ深いためか、勾配がうまく伝わっていないと思われたため、 BatchNormalizationを加えて、各層の平均を0に、分散を正規化した。 これにより、異なるノイズからは少なくとも異なる画像が生成されるようになった。
def Discriminator(): act = keras.layers.advanced_activations.LeakyReLU(alpha=0.2) Dis = Sequential() Dis.add(Dense(input_dim=784, units=1024, kernel_regularizer=l1_l2(1e-5, 1e-5))) Dis.add(act) Dis.add(Dense(units=512, kernel_regularizer=l1_l2(1e-5, 1e-5))) Dis.add(act) Dis.add(Dense(units=256, kernel_regularizer=l1_l2(1e-5, 1e-5))) Dis.add(act) Dis.add(Dense(units=1, kernel_regularizer=l1_l2(1e-5, 1e-5))) Dis.add(Activation("sigmoid")) discriminator_optimizer = SGD(lr=0.1, momentum=0.1, decay=1e-5) Dis.compile(loss="binary_crossentropy", optimizer=discriminator_optimizer) return Dis
2つのネットワークを組み合わせたGAN
def Generative_Adversarial_Network(generator_model, discriminator_model): GAN = Sequential() GAN.add(generator_model) discriminator_model.trainable=False GAN.add(discriminator_model) gan_optimizer = SGD(0.1, momentum=0.3) GAN.compile(loss="binary_crossentropy", optimizer=gan_optimizer) return GAN
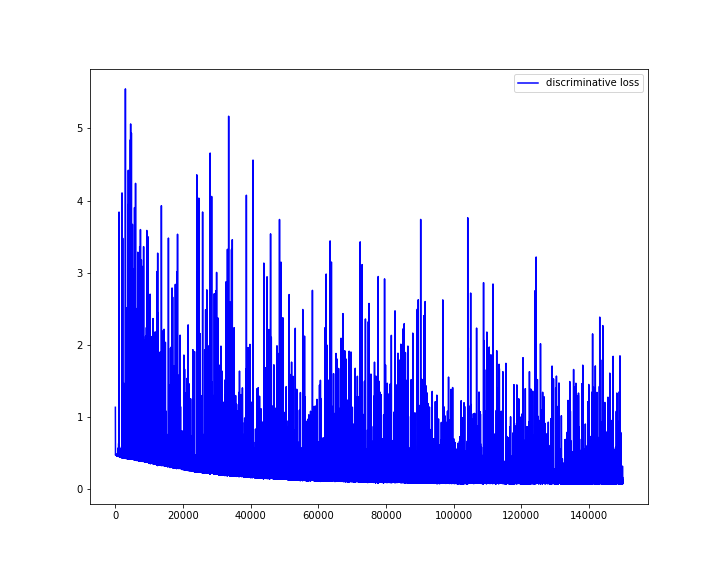
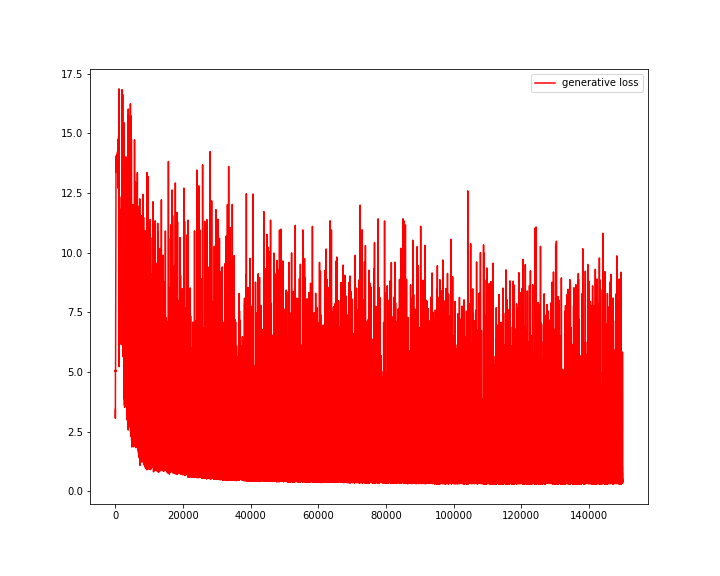
学習結果
loss関数
の学習では、真のデータと
の生成したデータの識別性能を高めていく。
の学習では、GAN全体のlossを小さくする。
生成データ
0epoch時点

1万epoch時点

5万epoch時点

15万epoch時点

gifアニメを見ると、あまり安定していないのがわかる。
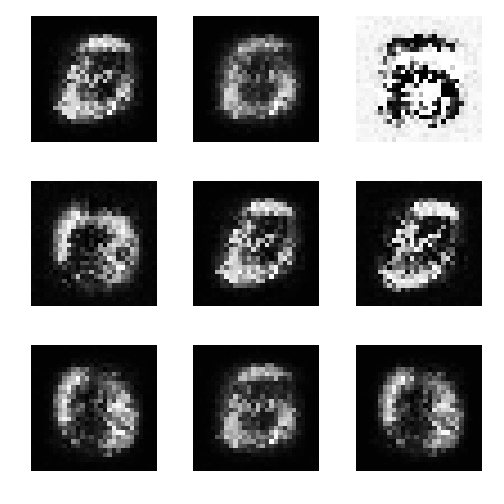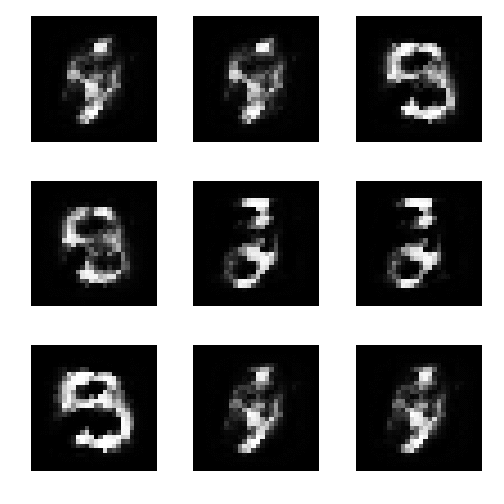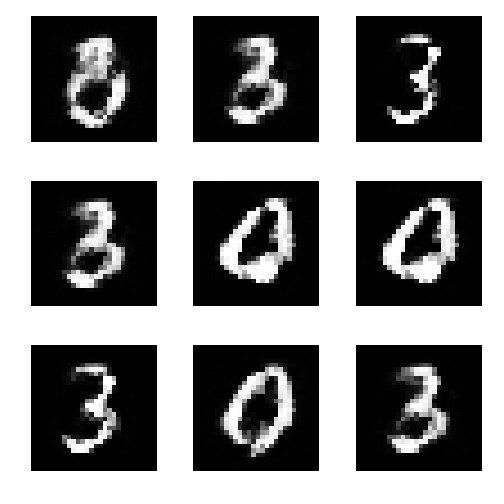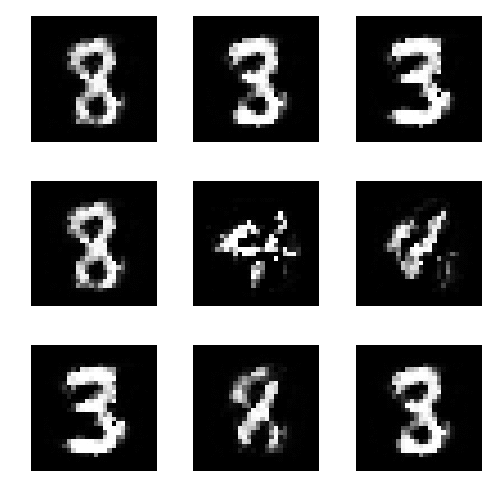
実装はgithubにおいておく. https://github.com/Ujitoko/keras_trial/tree/master/Generative_Adversarial_Net
この続きの取組みとして,DCGANも試してみた.↓
Deep Convolutional GANs(DCGAN)をkerasで実装して、いらすとや画像を生成する - 緑茶思考ブログ