Kullback-Leibler(KL) diviergence
同じ確率変数xに対する2つの確率分布P(x)とQ(x)があるとき、 これらの確率分布の距離をKullback-Leibler(KL) divergenceを使い評価できる。
KL divergenceは以下の式で表される。
$$
\begin{align}
D_{KL}(P||Q) &= \mathbb{E}_{x \sim P}[log \frac{P(x)}{Q(x)}] \\
&= \mathbb{E}_{x \sim P}[log P(x) - log Q(x)] \\
&= \int_{x} P(x) (log P(x) - log Q(x))
\end{align}
$$
このKL divergenceは交差エントロピーで以下のように表すこともできる。
$$
D_{KL}(P||Q) = -\mathbb{H}(P) + -\mathbb{H}(P,Q)
$$
KL divergenceには使い勝手のいい性質がいくつかある。
一つは非負性。どのようなP,Qに対しても非負の値となる。
(証明はこのサイトを参照。非常に分かりやすいです)
PとQが同じ分布となる場合にのみ、KL divergenceは0となる。
ただKL divergenceは対称性がない(PとQを交換したら等価でない)ため、距離の公理を満たさない。
家から駅までの距離と駅から家までの距離は普通同じはずなのだが、KL divergenceでは対称ではない。
そのため、か
のどちらを使うかは重要な選択となる。
KL divergenceのイメージをつかむため、 同じ分散をもつ正規分布P,Qを徐々にずらして、KL divergenceを計算したものを以下に示す。

分布の重なりが小さくなるにつれて、KL divergenceが小さくなるのがわかる。
Jensen-Shannon divergence
上記のKL divergenceは非対称なので不便。
そこで対称となるように定義した指標としてJensen-Shannon(JS) divergenceがある。
$$
D_{JS} = \frac{1}{2}D_{KL}(P||M) + \frac{1}{2} D_{KL}(Q||M) \\
(ただし
M(x) = \frac{P(x) + Q(X)}{2})
$$
上と同じ分布を使ってJS divergenceを見てみる。
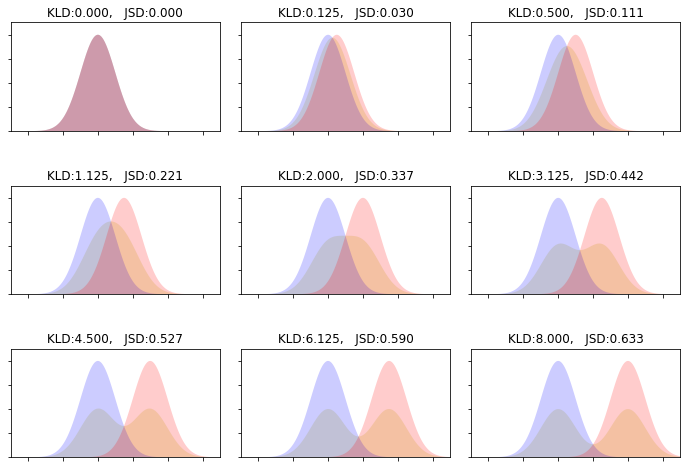
赤と青がそれぞれと
の分布で、
黄色っぽくなっている分布が
と
の平均の分布で
である。
KL divergenceの場合と同じく、赤と青の分布が離れるにつれてJS divergenceの値も大きくなっている。
Bengio本にはJS divergence載っていないが、Murphy本には載っているらしい…
追記) 一応コードを残しておく
import matplotlib.pyplot as plt import numpy as np from scipy.stats import norm, entropy x = np.linspace(-10.0, 10.0, 10000) # 図形サイズ plt.figure(figsize=(12,8)) # 3x3のsubplot for i in np.arange(3): for j in np.arange(3): index = i*3 + j # 各確率分布を定義 p = norm.pdf(x, loc=0, scale=1) q = norm.pdf(x, loc=index*0.5, scale=1) # pとqの平均の確率分布 m = (p+q)/2 # KL divergenceとJS divergenceの計算 kl = entropy(p, q) kl_pm = entropy(p, m) kl_qm = entropy(q, m) js = (kl_pm + kl_qm)/2 # subplot plt.subplot(3,3,i*3+j+1) # 図形塗りつぶし plt.fill_between(x, m, facecolor="y", alpha=0.2) plt.fill_between(x, p, facecolor="b", alpha=0.2) plt.fill_between(x, q, facecolor="r", alpha=0.2) # 以下は整形 plt.xlim(-5, 7) plt.ylim(0,0.45) plt.title("KLD:{:>.3f}".format(kl) + ", JSD:{:>.3f}".format(js)) plt.tick_params(labelbottom="off") plt.tick_params(labelleft="off") plt.subplots_adjust(wspace=0.1, hspace=0.5) plt.show()