【CS231n】Convolutional Neural Networks: Architectures, Convolution / Pooling Layers

Stanford大の教材CS231nを使ってNNやCNNを学んでいる．
この記事では、CNNの概要を学ぶ。

CNNはこれまで学んできたNNとほとんど変わらない。
CNNの特徴は、入力データがほぼ決まって画像であることである。
画像の性質を使ったエンコードを用いて特徴量を抽出していく。

Architecture Overview

普通のNNはスケールしないので画像に向かない
  • CIFAR-10データセットだと画像サイズは[32 * 32 * 3]なので、
    はじめのNeural Networkは32323=3072の重みパラメータをもつ。
    • これ以上大きくできない
    • [200 * 200 * 3]の画像だと、120,000のパラメータ数になる
3次元ニューロン
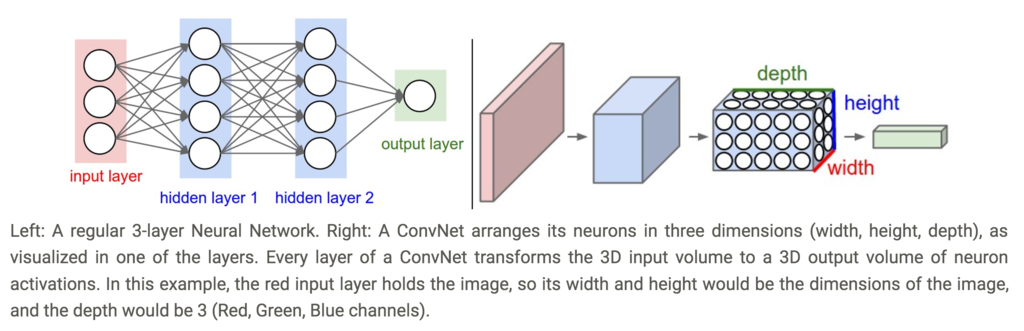f:id:yusuke_ujitoko:20170116221646p:plain (CS231nより引用)

Layers used to build ConvNets

  • ConvNetを構成する3種類のレイヤー
    • Convolutional Layer
    • Pooling Layer
    • Fully-Connected Layer
  • これらを組み合わせてConvNet architectureをつくる
例
  • CIFAR-10用のConvNetは[INPUT - CONV- RELU - POOL - FC]からなる
  • INPUT [32 * 32 * 3]
    • 生データ
  • CONV layer
    • 重みと入力の畳み込みを演算する
    • 出力は、12個のフィルタを使うとき[32 * 32 * 12]となる
  • RELU layer
    • 要素ごとに{\max(0,x)}を計算する
    • 出力サイズは変わらず[32 * 32 * 12]
  • POOL layer
    • downsampling operation
    • 出力サイズは[16 * 16 * 12]
  • FC(fully-connected) layer
    • クラスのスコアを計算する
    • 出力サイズは[1 * 1 * 10]
f:id:yusuke_ujitoko:20170116225713p:plain (CS231nより引用)

以降は、それぞれのレイヤについて詳細にみていく

ConvNet Layers

脳やニューロンのアナロジーなしで議論してみる
  • CONV layerのパラメータ群は学習可能なフィルタからなる
  • 各フィルタは空間性をもつ（depthだけ最大となっている）
  • 例
    • [5 * 5 * 3]のサイズのConvNet
    • forward passでは、端から端へフィルタをslideさせて、入力との内積をとり、2次元のデータ(activation map)を得る
    • 12個のフィルタがあるときには、それぞれ2次元のactivation mapを得る。
脳とみなして議論してみる
  • 3次元の出力は、左右のニューロンと共通のパラメータを持つものと解釈できる。
局所的な結合性（Local Connectivity）
  • 画像のような巨大な入力のときには、全ニューロンが全ニューロンと結合するのは実際的ではない
  • その代わりに局所的に結合し合う
例1
  • [32 * 32 * 3]のサイズの入力のとき
    • receptive fieldが[5 * 5]とすると、ConvLayerは[5 * 5 * 3]の重みをもつ。

例2
  • [16 * 16 * 20]のサイズの入力のとき
    • receptive fieldが[3 * 3]とすると、ConvLayerは[3 * 3 * 20]の重みをもつ。
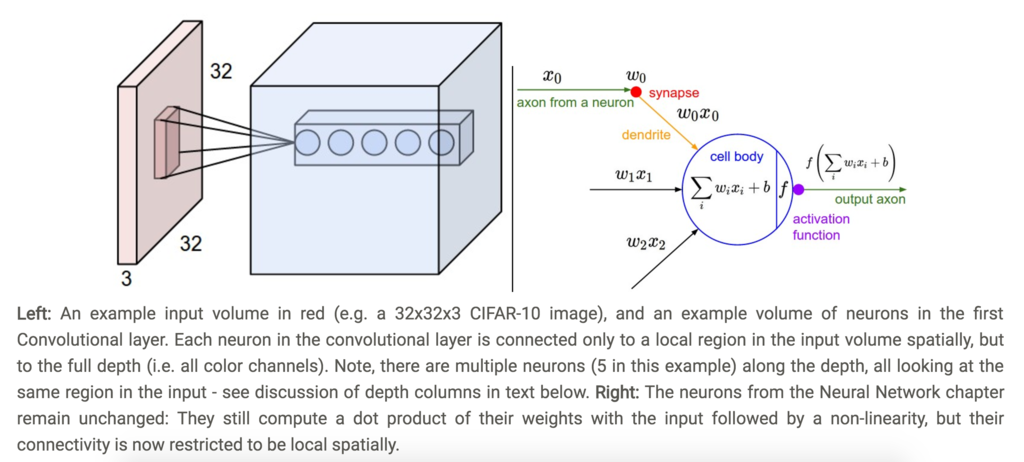f:id:yusuke_ujitoko:20170117211338p:plain (CS231nより引用)
Spatial arrangement
  • 出力サイズを決めるハイパーパラメータは3つある
    • depth
    • stride
    • zero-padding

  • depth
    • 使いたいフィルタの数を示す
  • stride
    • フィルタをスライドする幅をきめる
  • zero-padding
    • 境界の周りに0を詰めることで、出力サイズを入力サイズに保てる。

  • 出力サイズを入力サイズ{W}、receptive field size{F}、stride{S}、zero-paddingの幅{P}を使って計算できる
    • {(W-F+2P)/S + 1}
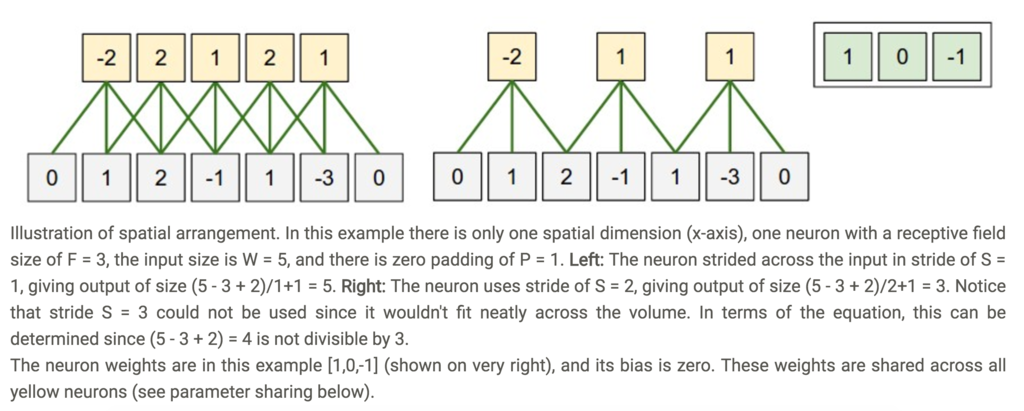f:id:yusuke_ujitoko:20170117212556p:plain (CS231nより引用)
Parameter sharing
  • depth sliceした二次元上のニューロンは同じ重みとバイアスを持たせる。
    • これにより、パラメータの爆発を防げる。
    • これが畳み込みと言われる所以であり、そのときの重みはfilterと呼ばれる
f:id:yusuke_ujitoko:20170117222227p:plain (CS231nより引用)
  • ただし、ときにはparameter sharingは上手く行かないことがある
    • たとえば、入力データが中央に寄っている場合
      (顔など）
行列積として実装する
  • im2colという操作がある
    • これはフィルタ（重み）にとって都合の良いように入力データを展開する関数
      • たとえば、[2272273]の入力データが、[11113]のフィルタで畳み込み演算されるとき、
      • 入力データのうち[11113]分のブロック部分を、ベクトルに展開する。
      • この操作を畳み込み積分だけ行う（227-11)/4+1=55回
    • 同じようにフィルタもベクトルに展開する
  • こうして入力データと重みのベクトルをそれぞれ行列として作る。
  • あとは行列積を行う

  • この手法はメモリサイズで不利だが、それ以上に計算はBLASなどを使えば高速に行える。
backpropagation
  • ConvNetのbackpropはそのままでよい？
Dilated convolution
  • Fisher Yu and Vladlen Koltunの論文で、dilationと呼ばれるCONV layerのハイパーパラメータが紹介されている
  • 例
    • フィルタサイズ3のフィルタを入力に適用する
      • dilation of 0のときw[0]x[0] + w[1]x[1] + w[2]*x[2]
      • dilation of 1のときw[0]x[0] + w[1]x[2] + w[2]*x[4]
  • スケールが異なる受容野を効率的に扱える。

Pooling Layer

  • Conv layersの中にPooling layerを挿入するのは一般的
  • 目的
    • パラメータの空間サイズを減らす
    • 過学習を制御すること

General pooling
  • max pooling以外にも、average poolingがあるが近年max poolingの方が使われつつある
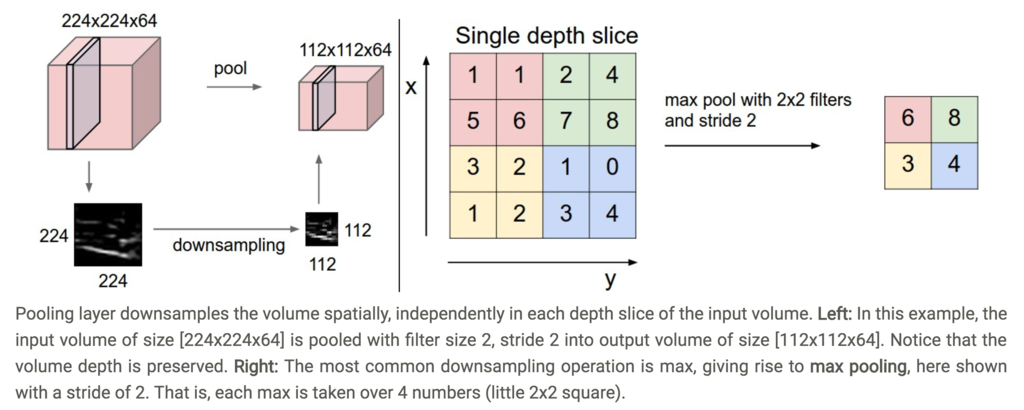f:id:yusuke_ujitoko:20170117231227p:plain (CS231nより引用)
pooling layerを取り除く
  • 多くの人がpooling operationを嫌って、取り除こうとしている.
  • たとえば、
  • パラメータ削減するために、CONV layerで使うstrideを大きくすることを提案している

Normalization Layer

Converting FC layers to CONV layers

  • 互いに変換可能

ConvNet Architectures

Layer Patterns

  • 一般的なConvNetの構造
    • CONV-RELU layersがあり、その後でPOOL layersがある。
    • これを繰り返し、画像が小さくする
    • ある所まで来たら、全結合層へ移行する。

INPUT -> [[CONV -> RELU]N -> POOL?]M -> [FC -> RELU]*K -> FC

  • 小さいフィルタのCONVを繰り返すほうが、大きいフィルタのCONV1つを使うよりも有利
    • CONVを繰り返すことで非線形性を表現できる
    • 同じサイズの出力を得る場合にも、パラメータが小さくて済む 　

      Layer Sizing Patterns

Case studies

  • 名前の付いたCNNが色々ある。

  • LeNet
    • 1990年代に発表された。
      LeNet
  • AlexNet
    • 2012年にImageNet ILSVRC challengeで驚異的な成績を残して有名になった.
    • LeNetに似ているが、より深く大きくなったもの
  • ZF Net
    • ILSVRC 2013の勝者
    • ZFNet
  • GoogLeNet
    • ILSVRC 2014の勝者
    • Inception Module
  • VGGNet
  • ResNet
    • ILSVRC 2015の勝者
    • Residual Network

Computational Considerations

理解できなかった内容

Moreover, we would almost certainly want to have several such neurons, so the parameters would add up quickly! Clearly, this full connectivity is wasteful and the huge number of parameters would quickly lead to overfitting.

The brain view. If you’re a fan of the brain/neuron analogies, every entry in the 3D output volume can also be interpreted as an output of a neuron that looks at only a small region in the input and shares parameters with all neurons to the left and right spatially (since these numbers all result from applying the same filter). We now discuss the details of the neuron connectivities, their arrangement in space, and their parameter sharing scheme.

Backpropagation. The backward pass for a convolution operation (for both the data and the weights) is also a convolution (but with spatially-flipped filters). This is easy to derive in the 1-dimensional case with a toy example (not expanded on for now). 1x1 convolution. As an aside, several papers use 1x1 convolutions, as first investigated by Network in Network. Some people are at first confused to see 1x1 convolutions especially when they come from signal processing background. Normally signals are 2-dimensional so 1x1 convolutions do not make sense (it’s just pointwise scaling). However, in ConvNets this is not the case because one must remember that we operate over 3-dimensional volumes, and that the filters always extend through the full depth of the input volume. For example, if the input is [32x32x3] then doing 1x1 convolutions would effectively be doing 3-dimensional dot products (since the input depth is 3 channels).

まとめ

yusuke-ujitoko.hatenablog.com