Stanford大の教材CS231nを使ってNNやCNNを学んでいる.
本記事では,Optimizationについて,下記項目を中心に扱う.
- Stochastic Gradient Descent
Introduction
- 前セクションの展開
- 画像の生ピクセルをクラススコアにマッピングするscore function
- パラメータの質を測定するloss function
- 真のラベルとどのくらい離れているか
- SVMとかSoftmaxとか色々ある
$$ \begin{align} L &= \frac{1}{N} \sum_{i}{L_{i}} + \alpha R(W) \\ &= \frac{1}{N}\sum_{i}\sum_{j \neq y_{i}}{\max(0, f(x_{i}; W)_{j} - f(x_{i}; W)_{y_{i}} + 1 )}+ \alpha \sum_{k}\sum_{l} {W_{k,l}^2} \end{align} $$
- ここからは,上記loss functionを最小にするような
を求めるoptimization(最適化)について導入する
Visualizing the loss function
- loss functionをray(1 dimension or 2 dimensions)に沿って切断すると,可視化できる
- 手続き
- ランダムな重み行列
を生成する
- ランダムな方向
を生成する
- この方向に沿ってlossを計算する.
具体的には,を
を動かしてプロットする(下図)
- ランダムな重み行列
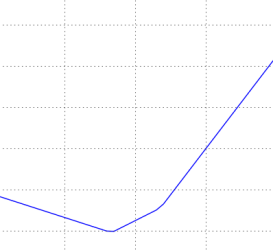 (CS231nより引用)
(CS231nより引用)
- 2つの方向に拡張してlossを計算する
具体的には,を
を動かしてグラフ化する(下図)
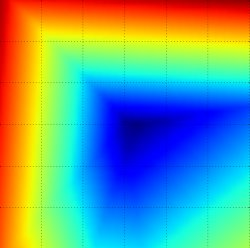 (CS231nより引用)
(CS231nより引用)
- loss functionの区分線形構造(piecewise-linear structure)を数学で解く
- 例
$$ L_{i} = \sum_{j \neq y_{i}}{\max(0, w_{j}^T x_{i} - w_{y_{i}}^T x_{i}+ 1 )} $$
- これは
の線形関数となっている
- 単純な例を考えてみる
- 1次元の点と3つのクラスからなる
- SVMのlossは以下のようになる
$$ \begin{align} L_{0} &= \max(0, w_{1}^T x_{0} - w_{0}^T x_{0}+ 1 ) + \max(0, w_{2}^T x_{0} - w_{0}^T x_{0}+ 1 ) \\ L_{1} &= \max(0, w_{0}^T x_{1} - w_{1}^T x_{1}+ 1 ) + \max(0, w_{2}^T x_{1} - w_{1}^T x_{1}+ 1 ) \\ L_{2} &= \max(0, w_{0}^T x_{2} - w_{2}^T x_{2}+ 1 ) + \max(0, w_{1}^T x_{2} - w_{2}^T x_{2}+ 1 ) \\ L &= (L_0 + L_1 + L_2)/3 \end{align} $$
- この例は1次元なので,
,重み
は数値
- たとえば,
に着目すると,関数は
の線形関数となっている
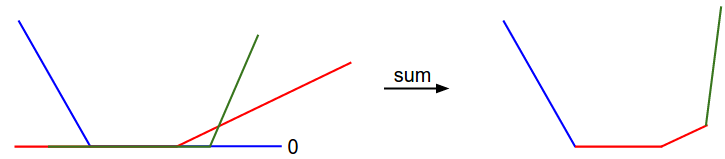
(CS231nより引用)
- SVM cost 関数は凸関数の1種
- fをニューラルネットワークの式に拡張すると、凸関数ではなくなる。
Optimization
- loss functionは重み
の質を数値化できる
- 最適化(optimization)の目的は、loss functionを最小にする
を探すこと
- ここからステップを踏んで、loss functionを最適化するアプローチを発展させていく
戦略1: Random search
- ランダムな重みを試して、どれが一番いいか決める手法(明らかに悪手)
# assume X_train is the data where each column is an example (e.g. 3073 x 50,000) # assume Y_train are the labels (e.g. 1D array of 50,000) # assume the function L evaluates the loss function bestloss = float("inf") # Python assigns the highest possible float value for num in xrange(1000): W = np.random.randn(10, 3073) * 0.0001 # generate random parameters loss = L(X_train, Y_train, W) # get the loss over the entire training set if loss < bestloss: # keep track of the best solution bestloss = loss bestW = W print 'in attempt %d the loss was %f, best %f' % (num, loss, bestloss) # prints: # in attempt 0 the loss was 9.401632, best 9.401632 # in attempt 1 the loss was 8.959668, best 8.959668 # in attempt 2 the loss was 9.044034, best 8.959668 # in attempt 3 the loss was 9.278948, best 8.959668 # in attempt 4 the loss was 8.857370, best 8.857370 # in attempt 5 the loss was 8.943151, best 8.857370 # in attempt 6 the loss was 8.605604, best 8.605604 # ... (trunctated: continues for 1000 lines)
- この方法だと、最も良い
を選んでも15.5%のaccuracyだった
- 完全にランダムに選ぶと10%であることを考えると、死ぬほど悪くはない方法かもしれない
- 反復的に改良していくこと(iterative refinement)は重要なアイデア
- 我々のアプローチではランダムに
を選び、それを反復的に改良していく
- 我々のアプローチではランダムに
- Blindfolded hiker analogy
- 重要なアナロジーとして、「最低地点を目指しながら、丘状を目隠しして歩くこと」を考える。
- CIFAR-10では丘は30730次元で、
の次元は3073*10。
- どの地点でもlossがある(標高)
戦略2:Random Local Search
- ランダムに少し動かして、もしそのときの勾配がマイナスだったら、移動する戦略
- 具体的には
- ランダムな重み
から始め
- 摂動
を生成し
のlossが低かったら、Wを更新する
- ランダムな重み
- 具体的には
W = np.random.randn(10, 3073) * 0.001 # generate random starting W bestloss = float("inf") for i in xrange(1000): step_size = 0.0001 Wtry = W + np.random.randn(10, 3073) * step_size loss = L(Xtr_cols, Ytr, Wtry) if loss < bestloss: W = Wtry bestloss = loss print 'iter %d loss is %f' % (i, bestloss)
- 1000回反復すると、accuracyは21.4%となった
- さきほど良いが、まだ無駄があり計算コストも高い
戦略3:Following the Gradient
- 戦略2ではlossを小さくする重み
の方向を探していた
- 実はいい方向を探すのはランダムでなくてよい
- もっとも勾配が急な方向を選べばよい
- この方向はloss fucntionの勾配と関連している
- hikingのアナロジーで言うと、坂がもっとも急な方向を選んで降りていくイメージ。
- 勾配は数学的に言うと、単純に微分である
(対象の関数がスカラーでなくベクトルの場合、偏微分という)$$ \frac{d f(x)}{d x} = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} $$
Computing the gradient
- 勾配を計算する方法は2つある
- 数値的勾配(numerical gradient)
- 収束が遅い
- 近似解
- 単純なアルゴリズム
- 解析的勾配(analytic gradient)
- 速い
- 正確
- 誤差を含みやすい
- 数値的勾配(numerical gradient)
- これら2つを見ていく
数値的に勾配を計算する
def eval_numerical_gradient(f, x): """ a naive implementation of numerical gradient of f at x - f should be a function that takes a single argument - x is the point (numpy array) to evaluate the gradient at """ fx = f(x) # evaluate function value at original point grad = np.zeros(x.shape) h = 0.00001 # iterate over all indexes in x it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite']) while not it.finished: # evaluate function at x+h ix = it.multi_index old_value = x[ix] x[ix] = old_value + h # increment by h fxh = f(x) # evalute f(x + h) x[ix] = old_value # restore to previous value (very important!) # compute the partial derivative grad[ix] = (fxh - fx) / h # the slope it.iternext() # step to next dimension return grad
- 実用上の考察
は小さければ小さいほどよいが、実用上はある程度小さい値であれば問題ない
- 理想的には、centered difference formulaで計算したほうが正しい。
- 微分がマイナスの方向に更新する
- loss functionが小さくなるよう
- step sizeの効果
- 勾配はどの方向が最も急か教えてくれるが、どのくらい遠くまで移動すべきかは教えてくれない
- 行き過ぎると坂を上ってしまう(下図)
- step size(learning rateともいう)の選択は、難しいハイパーパラメータの一つ
- 勾配はどの方向が最も急か教えてくれるが、どのくらい遠くまで移動すべきかは教えてくれない
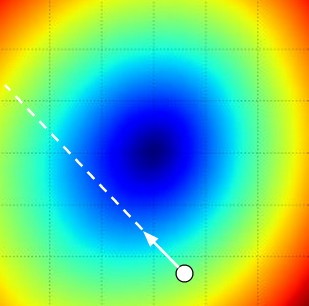 (CS231nより引用)
(CS231nより引用)
- 数値的勾配(numerical gradient)を算出するコスト
- ベクトルの次元数に比例してコストがかかる
- 今回の例だと一回の更新で30730回の計算が必要
- Neural Networksだと1000万個くらいパラメータがある...
- もっと良い解法が必要
- ベクトルの次元数に比例してコストがかかる
解析的に勾配を計算する
- 数値的な勾配計算はシンプルだが、近似解であり、高価であった
- 2つ目の方法は公式を使う解析的な方法
- 高速だが、実装がerror-prone
- そのため数値的勾配と答え合わせをする必要がある。これをgradient checkという
Gradient descent
- loss functionの勾配を計算できるので、反復的に勾配を計算して、重みを更新していく。
- これを勾配降下(Gradient descent)という
- Mini-batch gradient descent
- 大規模アプリケーションの場合、training dataがmillionのオーダーだったりする。
- そんなときは全体のtraining dataからバッチ(batches)を取り出してそれに対する勾配を計算する
- training dataに関連性があるため、この方法が上手くいく。
- mini-batch gradient descentの最たる例が、ミニバッチに1つの例しか含まない場合
Summary
 (CS231nより引用)
(CS231nより引用)
- loss functionを直観的にとらえるために,high-dimensional optimization landscapeを確認した
- もっとも勾配が小さい所を目指す
- 目の見えない登山者をアナロジーとして紹介
- SVM cost functionは線形で,bowlの形をしていた.
- iterative refinementでloss functionを最適化する.
- 重みの初期値はランダム
- lossが最小化するまで,ステップごとに最適値まで移動
- 関数の勾配(gradient)により,最も勾配が急な方向がわかる
- パラメータの更新には,step size(learning rate)の調整が必要
- step sizeが小さすぎると,収束は安定するが遅い
- step sizeが大きすぎると,収束は早いが不安定になる
- 勾配の計算を数値的に行うか解析的に行うかはトレードオフがある
- 数値的勾配
- シンプルだが,近似的で計算コストが大きい
- 解析的勾配
- 正確で高速だが,エラーが起きやすい
- 数値的勾配
- 上記の考察から通常,解析的勾配を使い,その結果を数値的勾配と比較するgradient checkを行う
- Gradient Descent アルゴリズムの紹介
- 勾配を反復的に計算し,パラメータを更新
理解できなかった内容
It is clear from the equation that the data loss for each example is a sum of (zero-thresholded due to the max(0,−)max(0,−) function) linear functions of WW. Moreover, each row of WW (i.e. wjwj) sometimes has a positive sign in front of it (when it corresponds to a wrong class for an example), and sometimes a negative sign (when it corresponds to the correct class for that example). To make this more explicit, consider a simple dataset that contains three 1-dimensional points and three classes. The full SVM loss (without regularization) becomes: