【ゼロから作るDeep Learning】4章 ニューラルネットワークの学習

機械学習

本章では，ニューラルネットワークの学習を扱う．
学習とは「訓練データから最適な重みパラメータの値を自動で獲得する」こと．

データから学習する

データ駆動

  • 機械学習による手法
    • 人の介入を極力避ける
    • 集められたデータから答えを見つける

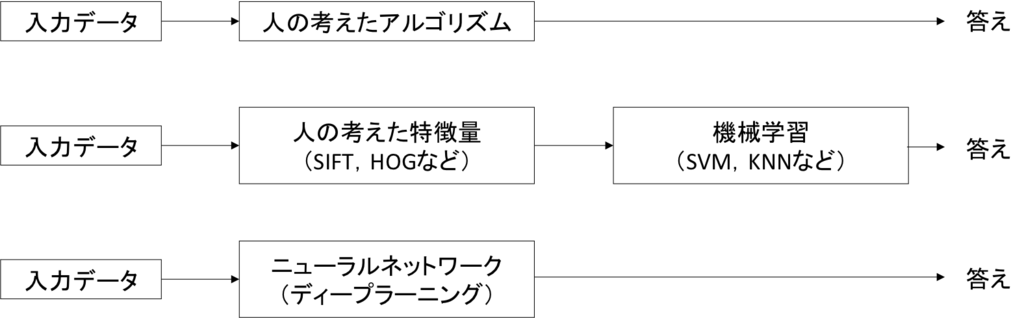
  • 特徴量
    • 入力データから本質的なデータを的確に抽出できるよう設計された変換器のこと
    • CVで有名な特徴量
      • SIFT
      • SURF
      • HOG
        • これらは「人」が設計した特徴量

  • ニューラルネットワーク
    • 特徴量も学習させる
    • すべての問題を同じ流れで得．
    • 対象とする問題に関係なく，データをそのまま生データとして，"end-to-end"で学習できる

f:id:yusuke_ujitoko:20161230173310p:plain:w650

  • 訓練データとテストデータを分ける必要性
    • モデルの汎化能力を正しく評価したいため
      • まだ見ぬデータに対しての能力
  • あるセットにだけ過度に対応した状態を過学習という(overfitting)

損失関数

  • 損失関数（loss function）

  • 交差エントロピー誤差
    • { E = -\sum_{k} {t_k \log{y_k}} }
    • {y_k}はニューラルネットワークの出力，{t_k}は正解ラベル，{k}はデータの次元数を表す
    • {t_k}は正解ラベルとなるインデックスだけが1で，その他は0であるとする．
    • そのまえ，実質的に正解ラベルが1に対応する出力の自然対数を計算するだけになる.

  • 訓練データすべての損失関数の和を求めたいとすると，交差エントロピー誤差の場合は以下の式のようになる.
    • { E = -\frac{1}{N} \sum_{n} \sum_{k} {t_{nk}} \log{y_{nk}} }

  • すべてのデータを対象にして，損失関数の和を求めるには時間がかかる．
    そこで一分のデータを選び出し，その一部のデータを全体の近似として利用
  • この学習方法をミニバッチ学習と呼ぶ．

  • なぜ認識精度そのものでなく損失関数を設定するのか
    • 勾配法を使うため．
    • 認識精度だと勾配が殆どの場所で0になる

勾配法（gradient method）

  • 勾配が指す方向は，各場所において関数の値を最も減らす方向
  • 勾配法を数式で表すと下記のようになる．
    • {\eta}は更新の量を表す．
      • ニューラルネットの学習においては学習率とも呼ばれる.
      • 高すぎても低すぎても「良い場所」にたどり着けない.

{ x_0 = x_0 - \eta \frac{\partial f}{\partial x_0} }

{ x_1 = x_1 - \eta \frac{\partial f}{\partial x_1} }

ニューラルネットワークの学習アルゴリズム

  • 前提
    • ニューラルネットワークには適応可能な重みとバイアスがある．
    • ミニバッチ
      • 訓練データの中からランダムに一部のデータを選び出す
    • 勾配の算出
      • ミニバッチの損失関数を減らすために，各重みパラメータの勾配を求める
    • パラメータの算出
      • 重みパラメータを勾配方向に微小量だけ更新する
    • 繰り返す

  • 確率的勾配降下法（stochastic gradient descent）
    • 確率的に無作為に選びだしたデータを使って，パラメータを更新する
    • SGD

本章で学んだこと

  • 機械学習で使用するデータセットは，訓練データとテストデータに分けて使用する
  • 訓練データで学習を行い，学習したモデルの汎化能力をテストデータで評価する
  • ニューラルネットワークの学習は，損失関数を指標として，損失関数の値が小さくなるように，重みパラメータを更新する
  • 重みパラメータを更新する際には，重みパラメータの勾配を利用して，勾配方向に重みの値を更新する作業を繰り返す
  • 微小な値を与えたときの差分によって微分を求めることを数値微分という
  • 数値微分によって，重みパラメータの勾配を求めることができる
  • 数値微分による計算には時間がかかるが，その実装は簡単である．一方，自称で実装するやや複雑な誤差逆伝播法は，高速に勾配を求めることができる．

後で調べておくこと

  • CVで有名な特徴量について
    • SIFT
    • SURF
    • HOG
  • パーセプトロンの収束定理
    • 有限回の学習によって，線形分離可能な問題が解けること

yusuke-ujitoko.hatenablog.com