Tutorial on Variational Autoencoders(VAEs)を読み解いていこうと思う。
先人たちによる日本語の詳細な解説はネット上にゴロゴロあるので、
本記事は自分自身の理解のためのメモという位置づけ。
潜在変数
生成モデルは、高次元空間におけるデータ
の分布
自体をモデル化するもののこと。
例えば、MNISTのような0〜9からなる手書き文字を生成する目的の生成モデルがある．
このとき、モデルの生成対象は0〜9の文字なので、
モデルはまずどの文字を生成するかを決めて、その決定のもとでデータを生成するものだ，と仮定してみる。
このときの予め決定しておくパラメータのことを潜在変数(latent variable) 
と呼ぶ。
モデルが文字を描く前に、を[0,…,9]からランダムにサンプリングするというイメージ．
なぜ「潜在」と呼んでいるかというと、どの潜在変数が文字を生成したかについては必ずしも知っておく必要がないため。
潜在変数を決める確率分布を
とする。
固定のパラメータ
のもとで、ランダムにサンプリングしたから、を生成する。
このが訓練データのものとよく一致すればよい生成モデルと言えそう．
数学的に記述すると、次のようになる。
$$
\begin{equation}
P(X) = \int P(X \, | \, z;\theta) P(z) dz \tag{1}
\end{equation}
$$
訓練データの周辺尤度を最大化することで，潜在変数を推定する．
VAEでは、
はガウス分布をよく使う。
この場合のガウス分布は
となる。
VAEs
VAEはいわゆるAutoencoderとはあまり関係がない。
ではなぜAutoencoderと呼ばれているかというと，最終的な目的関数を構成するのがencoderとdecoderからなるから．
上記の(1)を解くにあたって、VAEは以下の2つの問題を解決しなくてはならない。
- 潜在変数をどう定義するか（どのような情報を表現するものと定義するか）
- 潜在変数の積分をどう扱うか。
1つめの問題は「文字の角度」「文字のストローク」「ストロークの太さ」「文字のスタイル」…など様々な性質が関わって複雑なため、できれば直接の表す情報を決定するのは避けたい。
VAEではこの問題に対して、変わったアプローチをとっている。
それは、を単純な分布、例えば正規分布
からサンプリングするというもの。
本当にこのアプローチは正しいのだろうか。
実は
次元のどのような分布であっても、正規分布からサンプルされた個の変数を複雑な関数でマッピングすれば表現可能なのである。
例として以下の図のようなリング状の二次元空間状の分布を得たい場合を考える。
正規分布からサンプルされたを、
で写像すると、うまいことリング状になる。
(arxiv論文から引用)
したがって、表現力豊かな関数があるのであれば、normally-distributedなを用いて、目的の分布を得ることができ、訓練データを表現できる。
を計算するためのコンセプトは明快。
- をサンプリングする(
![{\left[z_{1}, \cdots, z_{n} \right] }](http://chart.apis.google.com/chart?cht=tx&chl=%7B%5Cleft%5Bz_%7B1%7D%2C%20%5Ccdots%2C%20z_%7Bn%7D%20%5Cright%5D%20%7D)
)
を計算する
ここでの問題は、
高次元空間の場合、正確にを推定するには、
が非常に大きくなってしまうということ。
目的関数の設定
(1)式を簡単に計算する方法はなにかないだろうか？
よく考えると、大抵のに対して、
はほぼ0となることに気づく。
大抵のはなにも寄与しない。
VAEはこの考え方を利用していて、を生成するようなのみをサンプリングしようとする。
そこで
という新たな関数を考える。
この関数は、のもとで、の分布を与えるもので、逆から考えるとそのは結局を生成するようなものである。
このようなの空間は事前確率において極めて小さい。
これにより、例えば
の計算が簡単になる。
一方、の計算は簡単になるだろうか。
とりあえず最初にしてみるのはとの関係付けである。
との関係は、変分ベイズで片付けられる。
まずと
間のKL divergenceを任意の
に対して定義する。
$$
D \left[ Q(z) \mid\mid P(z \mid X) \right] = \mathbb{E}_{z \sim Q} \left[ \log Q(z) - log P(z \mid X) \right]
$$
この式に対して、ベイズの定理を適用して変換して、さらにに無関係な項を期待値からはずす操作を施す。
$$
D \left[ Q(z) \mid\mid P(z \mid X) \right] = \mathbb{E}_{z \sim Q} \left[ \log Q(z) - \log P(X \mid z) - \log P(z) \right] + \log P(X)
$$
両辺にマイナスをかけて、期待値の項の中身の一部をKL divergenceに書き換える。
$$
\log P(X) - D \left[ Q(z) \mid\mid P(z \mid X) \right] = \mathbb{E}_{z \sim Q} \left[ \log P(X \mid z) \right] - D \left[ Q(z) \mid\mid P(z) \right]
$$
は固定値であり、はあらゆる分布がありうることに注意しておく。
を推論することに興味があるため、に依存するようなを構築したい。
それはつまり![{D \left[ Q(z) \mid\mid P(z \mid X) \right]}](http://chart.apis.google.com/chart?cht=tx&chl=%7BD%20%5Cleft%5B%20Q%28z%29%20%5Cmid%5Cmid%20P%28z%20%5Cmid%20X%29%20%5Cright%5D%7D)
が小さくなるような場合。
$$
\begin{equation}
\log P(X) - D \left[ Q(z \mid X) \mid\mid P(z \mid X) \right] = \mathbb{E}_{z \sim Q} \left[ \log P(X \mid z) \right] - D \left[ Q(z \mid X) \mid\mid P(z) \right] \tag{2}
\end{equation}
$$
この式はVAEのコアになる部分なので詳しくみていく。
- 左辺のは最大化したい。
（一方で、左辺の
![{D \left[ Q(z \mid X) \mid\mid P(z \mid X) \right]}](http://chart.apis.google.com/chart?cht=tx&chl=%7BD%20%5Cleft%5B%20Q%28z%20%5Cmid%20X%29%20%5Cmid%5Cmid%20P%28z%20%5Cmid%20X%29%20%5Cright%5D%7D)
を最小化しつつ）
- 右辺は、勾配降下法でうまくを選んでいけば最適化できる。
この右辺の項はAutoencoderとみなせる。
がをにencodeし、一方
がからを復元しようとしている。
左辺では![{ D \left[ Q(z \mid X) \mid\mid P(z \mid X) \right]}](http://chart.apis.google.com/chart?cht=tx&chl=%7B%20D%20%5Cleft%5B%20Q%28z%20%5Cmid%20X%29%20%5Cmid%5Cmid%20P%28z%20%5Cmid%20X%29%20%5Cright%5D%7D)
を最小化しつつ、を最大化する。
は解析的に計算できない。
しかし、左辺の二項目の
は
に近づいていくことを考えてみる。
もし、の表現力が高く、と近い場合には、これらの間のKL divergenceは0になる。
この仮定のもとでは 
のみを最適化すればよい。
目的関数を最適化する
(2)の右辺をどのように最適化すればよいだろうか？
をどうするかという問いになるが、
普通は 
とする。
ここで
と
はパラメータを持つ任意の関数でデータから学習する。
実際、とはニューラルネットワークで決める。
この手法は計算量は小さいのが利点。
もうひとつの項は、![{D \left[ Q(z|X || P(z) \right]}](http://chart.apis.google.com/chart?cht=tx&chl=%7BD%20%5Cleft%5B%20Q%28z%7CX%20%7C%7C%20P%28z%29%20%5Cright%5D%7D)
はKL divergenceである。
多変量ガウス分布のKL divergenceは、次のようなclosed formで書ける。
$$
D [ \mathcal{N}(\mu_{0}, Σ_{0}) || \mathcal{N}(\mu_{1}, Σ_{1}) ] = \frac{1}{2} \bigl( tr(Σ_{1}^{-1} Σ_{0}) + (\mu_{1} - \mu_{0})^{T} Σ_{1}^{-1} (\mu_{1} - \mu_{0}) -k + \log(\frac{det Σ_{1}}{det Σ_{0}}) \bigr)
$$
今回に適用するとシンプルになる。
$$
D [ \mathcal{N}(\mu(X), Σ(X)) || \mathcal{N}(0,I) ] = \frac{1}{2} \bigl( tr(Σ(X)) + (\mu(X))^{T} (\mu(X) -k - \log det (Σ(X)) \bigr)
$$
さて、(2)の式に戻る。
(2)の右辺第一項に対する対応は、を１つサンプルして、それに基づくを
とみなすこととする。
最後に、データセット全体からサンプルをとって期待値を計算すると、
最適化したい式は次のようになる。
$$
\begin{equation}
E_{X \sim D} [ log P(X) - D[Q(z|X) || P(z|X)] ] = E_{X \sim D} [ E_{z \sim Q} [ log P(X | z)] - D[Q(z|X) || P(z) ]] \tag{3}
\end{equation}
$$
この式に基づいて勾配計算をするときには、期待値の中身を計算すればよい。
つまりと
をサンプルして、以下の勾配を計算する。
$$
log P(X|z) - D[ Q(z|X) || P(z) ]
$$
ところが実は![{\mathbb{E}_{z \sim Q}\left[log P(X \mid z)\right]}](http://chart.apis.google.com/chart?cht=tx&chl=%7B%5Cmathbb%7BE%7D_%7Bz%20%5Csim%20Q%7D%5Cleft%5Blog%20P%28X%20%5Cmid%20z%29%5Cright%5D%7D)
の計算に際して 深刻な問題 がある。
はだけでなくにも依存している。
しかし、(3)ではこの依存が消滅してしまっている。
VAEを上手く機能させるためには、を経た上で、がを復元させるようにする必要がある。
下図の（左）が問題を示している。
(arxiv論文から引用)
forward passは問題ない。
しかしbackpropagate時に、計算グラフが途切れているため、誤差をから
へ伝播することができない。
ここで reparameterization trick を使う。
この手法ではサンプリング操作の代わりにをの出力結果を元に関数で生成する。
具体的には、
と
のもとで、
としてを計算する。（ここで
は最適化とは無関係のハイパーパラメータ）
よって実際に勾配を取る式は次のようになる。
$$
E_{X \sim D} \left[ E_{\epsilon \sim N(0, I)}[log P(X|z = \mu(X) + Σ^{½} \odot \epsilon)] - D[Q(z|X) || P(z) ] \right]
$$
学習済みモデルを試すためには
新しいデータを生成したい時には、decoderに
を投入する。
単純にVAEからencoderを取り除く操作となる。
いらすとや画像を生成してみる
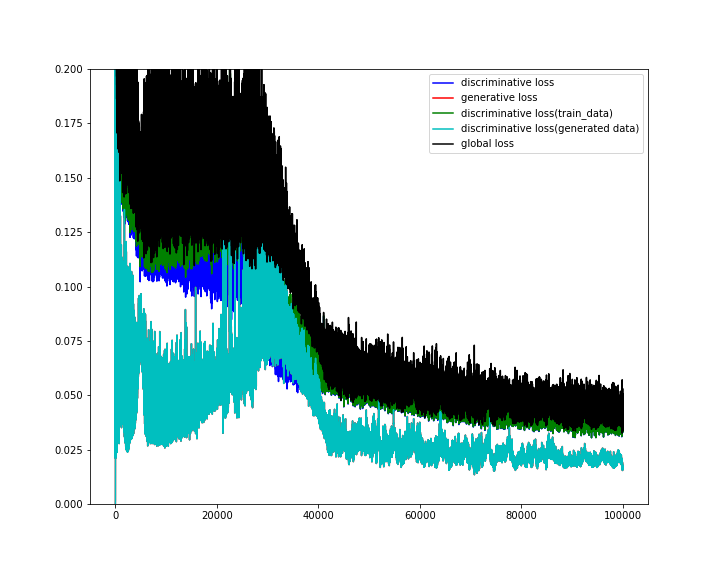
VAEをtensorflowで実装し，
いらすとや画像を生成してみた．
実装に誤りがあるのか，
現状うまく生成できなかった..
mode collapseが起きている。
(追記)
上の記述だと，
式変形を追いにくいので，全体の変形をまとめて書いてみる．
上よりも式変形を補った．
$$
\begin{align}
D \left[ Q(z) \mid\mid P(z \mid X) \right] &= \int Q(z) [\log Q(z) - \log P(z \mid X)] dz \\
&= \mathbb{E}_{z \sim Q} \left[ \log Q(z) - \log P(z \mid X) \right] \\
&= \mathbb{E}_{z \sim Q} \left[ \log Q(z) - \log P(X \mid z) - \log P(z) + \log P(X) \right] \\
&= \mathbb{E}_{z \sim Q} \left[ \log Q(z) - \log P(X \mid z) - \log P(z) \right] + \log P(X) \\
&= \mathbb{E}_{z \sim Q} \left[ \log Q(z) - \log P(z)\right] - \mathbb{E}_{z \sim Q} \left[ \log P(X \mid z) \right] + \log P(X) \\
&= D \left[ Q(z) \mid\mid P(z) \right] - \mathbb{E}_{z \sim Q} \left[ \log P(X \mid z) \right] + \log P(X)
\end{align}
$$
左辺と右辺を入れ替えて，
$$
\begin{align}
\log P(X) - D \left[ Q(z \mid X) \mid\mid P(z \mid X) \right] &= \mathbb{E}_{z \sim Q} \left[ \log P(X \mid z) \right] - D \left[ Q(z \mid X) \mid\mid P(z) \right] \\
\log P(X) & \geq \mathbb{E}_{z \sim Q} \left[ \log P(X \mid z) \right] - D \left[ Q(z \mid X) \mid\mid P(z) \right] = L(\theta, \phi; x)
\end{align}
$$
左辺を最大化する代わりに右辺を最大化する．
